题目内容
11.已知函数f(x)=ex-m,g(x)=ln(x+m),其中m>0(1)若P(x0,y0)是两个函数图象上的一个公共点,求证:x0=y0;
(2)若P(x0,y0)是两个函数图象上唯一的公共点,求实数m,x0的值;
(3)若两个函数图象无公共点,试问存在几条直线与它们都相切?请说明理由.
分析 (1)代入P的坐标,整理可得${e^{x_°}}+{x_°}={e^{y_°}}+{y_°}$,令u(x)=ex+x,运用导数判断单调性,即可得证;
(2)由(1)的结论,可得$m={e^{x_°}}-{x_°}$有唯一解,令h(x)=ex-x,求导判断单调性,即可求得m,x0的值;
(3)设存在公切线l与y=f(x)相切于点A(x1,y1),与y=g(x)切于点B(x2,y2),y=f(x)与y=g(x)无公共点,可得m<1,令$v(x)=x+({m-1})+\frac{-x+m-1}{e^x},x∈R$,求出导数,判断单调性,再由零点存在定理,即可判断.
解答 解:(1)证明:依题意,${e^{x_°}}-m=ln({{x_°}+m})={y_°}$,
则$m={e^{x_°}}-{y_°}={e^{y_°}}-{x_°}$
即${e^{x_°}}+{x_°}={e^{y_°}}+{y_°}$
令u(x)=ex+x,
∵u′(x)=ex+1>0,
∴u(x)在R上递增,∴x0=y0;
(2)由(1)可知方程${e^{x_°}}-m={x_°}$有唯一解,
即$m={e^{x_°}}-{x_°}$有唯一解,
令h(x)=ex-x,则由h′(x)=ex-1=0得x=0,
∵当x∈(-∞,0)时,h,(x)<0;
当x∈(0,+∞)时,h,(x)>0
∴h(x)在(-∞,0)递减,在(0,+∞)递增,
∴m=h(0)=1;
(3)设存在公切线l与y=f(x)相切于点A(x1,y1),
与y=g(x)切于点B(x2,y2),
则${e^{x_1}}=\frac{1}{{{x_2}+m}}=\frac{{{e^{x_1}}-m-ln({{x_2}+m})}}{{{x_1}-{x_2}}}$,
消x2得${x_1}+({m-1})+\frac{{-{x_1}+m-1}}{{{e^{x_1}}}}=0$,
∵y=f(x)与y=g(x)无公共点,∴m<1,
令$v(x)=x+({m-1})+\frac{-x+m-1}{e^x},x∈R$,
则v′(x)=$\frac{{e}^{x}+x-m}{{e}^{x}}$,
∵ex+x-m在R递增且e-1-1-m<0,e0+0-m>0,
∴存在t∈(-1,0)唯一使得et=m-t,
∴x∈(-∞,t),v(x)递减,x∈(t,+∞),v(x)递增,
又∵$v(t)=t+m-1+\frac{-t+m-1}{e^t}=t+m-1+\frac{-t+m-1}{m-t}=\frac{{({{m^2}-1})-{t^2}}}{m-t}<0$,
且$v({-2})=m-3+\frac{m+1}{{{e^{-2}}}}=m({1+{e^2}})+({{e^2}-3})>0$,
v(2)=m(1+e-2)+(1-3e-2)>0,
∴v(x)有且仅有2个零点,即y=f(x)与y=g(x)有2条公切线.
点评 本题考查导数的运用:求切线的方程,考查函数的单调性的运用,注意构造函数求导,判断单调性,考查运算能力,属于中档题.

| A. | 4 | B. | 4$\sqrt{2}$ | C. | 4$\sqrt{3}$ | D. | 4$\sqrt{5}$ |
| A. | 横坐标伸长到原来的2倍(纵坐标不变)得到 | |
| B. | 横坐标缩短到原来的$\frac{1}{2}$(纵坐标不变)得到 | |
| C. | 纵坐标伸长到原来的2倍(横坐标不变)得到 | |
| D. | 纵坐标缩短到原来的$\frac{1}{2}$(横坐标不变)得到 |
 如图,在直棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的重心G.
如图,在直棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的重心G.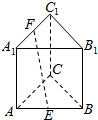 正三棱柱ABC-A1B1C1的各棱长都为2,E,F分别为AB、A1C1的中点,则EF的长是$\sqrt{5}$.
正三棱柱ABC-A1B1C1的各棱长都为2,E,F分别为AB、A1C1的中点,则EF的长是$\sqrt{5}$.