题目内容
5.已知函数f(x)=x3+ax2+bx+c,其导函数y=f′(x)的图象经过点(0,0),(2,0).(1)求a,b的值;
(2)求函数f(x)在区间[-1,3]上的最值.
分析 (1)求出函数的导函数,通过导函数经过的点,求解a,b的值.
(2)求出导函数的零点,得到函数的极值,与端点函数值比较,可得函数的最值.
解答 解:(1)函数f(x)=x3+ax2+bx+c,其导函数y=f′(x)=3x2+2ax+b,
导函数y=f′(x)的图象经过点(0,0),(2,0).
可得b=0,a=-3.
(2)由(1)可得f(x)=x3-3x2+c,f′(x)=3x2-6x,
令3x2-6x=0,解得x=0或x=2,
当x<0时,f′(x)>0,函数f(x)是增函数,
当0<x<2时,f′(x)<0,函数f(x)是减函数,
当x>2时,f′(x)>0,函数f(x)是增函数,
x=0函数取得极大值,x=2时函数取得极小值;
f(-1)=c-4,f(0)=c,f(2)=c-4,f(3)=c.
函数f(x)在区间[-1,3]上的最大值:c,最小值为:c-4.
点评 本题考查函数的对数的综合应用,函数的极值以及函数的最值的求法,考查计算能力.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
3.在以A(2,1),B(4,2),C(8,5)为顶点的三角形中,BC边上的高等于( )
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{6}{5}$ | D. | 2 |
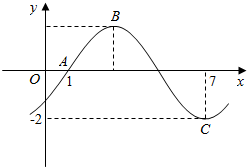 已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.