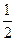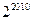题目内容
.(本小题满分12分)已知数列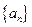 、
、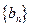 均为等差数列,设
均为等差数列,设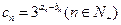 .
.
(1)数列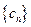 是否为等比数列?证明你的结论;
是否为等比数列?证明你的结论;
(2)设数列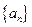 、
、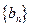 的前n项和分别为
的前n项和分别为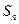 和
和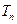 ,若
,若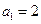 ,
,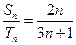 ,
,
求数列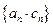 的前n项和 .
的前n项和 .
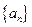 、
、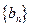 均为等差数列,设
均为等差数列,设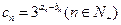 .
.(1)数列
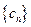 是否为等比数列?证明你的结论;
是否为等比数列?证明你的结论;(2)设数列
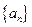 、
、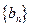 的前n项和分别为
的前n项和分别为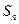 和
和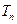 ,若
,若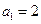 ,
,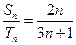 ,
,求数列
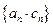 的前n项和 .
的前n项和 .(1)数列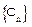 是等比数列
是等比数列
(2)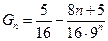
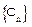 是等比数列
是等比数列(2)
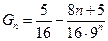
设数列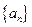 的首项为
的首项为 (其中
(其中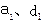 均为常数)
均为常数)
 (其中
(其中 均为常数)
均为常数)
则 .
.
 …………2分
…………2分
(1)数列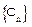 是等比数列.理由如下:
是等比数列.理由如下:
∵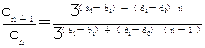
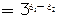 (常数)而
(常数)而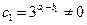
∴ 数列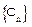 是等比数列,其中公比
是等比数列,其中公比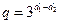 、首项为
、首项为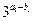 .……4分
.……4分
(2) 而
而

又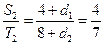 ,
, 
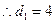 ,
, 
于是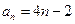 、
、 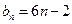 ,
, 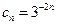 ,
,
 …………10分
…………10分
设数列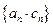 的前n项和为
的前n项和为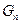 ,则利用错位相减法,
,则利用错位相减法,
易得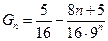 …………12分
…………12分
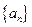 的首项为
的首项为 (其中
(其中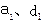 均为常数)
均为常数) (其中
(其中 均为常数)
均为常数)则
 .
. …………2分
…………2分(1)数列
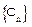 是等比数列.理由如下:
是等比数列.理由如下:∵
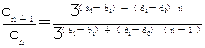
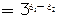 (常数)而
(常数)而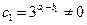
∴ 数列
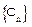 是等比数列,其中公比
是等比数列,其中公比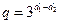 、首项为
、首项为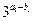 .……4分
.……4分(2)
 而
而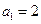

又
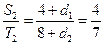 ,
, 
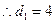 ,
, 
于是
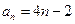 、
、 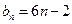 ,
, 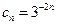 ,
,  …………10分
…………10分设数列
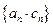 的前n项和为
的前n项和为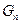 ,则利用错位相减法,
,则利用错位相减法,易得
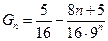 …………12分
…………12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
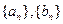 满足
满足
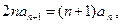 且
且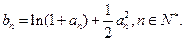
 ,
,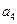 并求数列
并求数列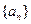 的通项公式;
的通项公式; ,证明
,证明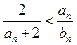 成立;
成立; 的前
的前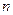 项和分别是
项和分别是 ,证明
,证明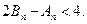
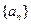 为等比数列,Sn是它的前n项和。若
为等比数列,Sn是它的前n项和。若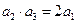 , 且
, 且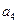 与2
与2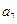 的等差中项为
的等差中项为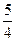 ,则
,则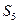 =
=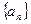 的前
的前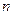 项和
项和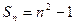 ,则
,则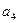 =" ( " )
=" ( " ) 中,
中, ,
, ,求此数列的通项公式;设
,求此数列的通项公式;设 是数列
是数列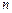 项和,求
项和,求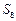 。
。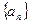 的前n项和为
的前n项和为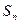 ,且满足
,且满足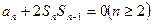 ,
,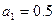 ,则
,则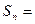 _
_ 中,
中, =1,
=1,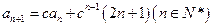 ,其中实数
,其中实数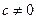 。
。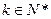 有
有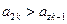 ,求c的取值范围。
,求c的取值范围。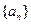 满足
满足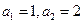 且
且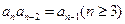 ,则
,则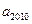 的值为
的值为