题目内容
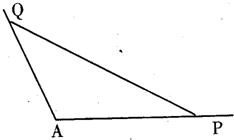
如图所示,角A为钝角,且sinA=
,点P、Q分别在角A的两边上.
(1)AP=5,PQ=3
,求AQ的长;
(2)设∠APQ=α,∠AQP=β,且cosα=
,求sin(2α+β)的值.
| 3 |
| 5 |
(1)AP=5,PQ=3
| 5 |
(2)设∠APQ=α,∠AQP=β,且cosα=
| 12 |
| 13 |

(1)∵∠A是钝角,sinA=
,∴cosA=-
,
在△APQ中,PQ2=AP2+AQ2-2AP•AQcosA,
∴45=25+AQ2-2×5AQ•(-
),
解得AQ=2或AQ=-10(舍)即AQ=2;
(2)由cosα=
,得sinα=
,
又sin(α+β)=sinA=
,cos(α+β)=-cosA=
,
∴sin(2α+β)=sin[α+(α+β)]=sinαcos(α+β)+cosαsin(α+β)=
•
+
•
=
.
| 3 |
| 5 |
| 4 |
| 5 |
在△APQ中,PQ2=AP2+AQ2-2AP•AQcosA,
∴45=25+AQ2-2×5AQ•(-
| 4 |
| 5 |
解得AQ=2或AQ=-10(舍)即AQ=2;
(2)由cosα=
| 12 |
| 13 |
| 5 |
| 13 |
又sin(α+β)=sinA=
| 3 |
| 5 |
| 4 |
| 5 |
∴sin(2α+β)=sin[α+(α+β)]=sinαcos(α+β)+cosαsin(α+β)=
| 5 |
| 13 |
| 4 |
| 5 |
| 12 |
| 13 |
| 3 |
| 5 |
| 56 |
| 65 |

练习册系列答案
相关题目
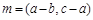 ,
,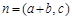 ,且
,且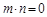
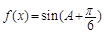 的值域.
的值域. 题
题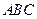 的内角
的内角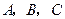 的对边分别为
的对边分别为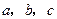 ,
,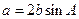 .(Ⅰ)求
.(Ⅰ)求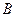 的大小;(Ⅱ)求
的大小;(Ⅱ)求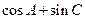 的取值范围.
的取值范围.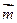 =(sinB,1-cosB),且与向量
=(sinB,1-cosB),且与向量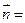 (2,0)所成角为
(2,0)所成角为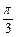 ,其中A, B, C是⊿ABC的内角.
,其中A, B, C是⊿ABC的内角.
 的内角
的内角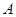 与
与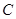 互补,
互补,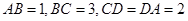 .
.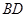 ;
;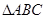 中,若
中,若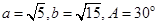 ,则边c的长度等于( ).
,则边c的长度等于( ).
