题目内容
4.已知命题:“?x∈[-1,1],使等式m=x2-x成立”是真命题.(1)求实数m的取值集合M;
(2)设不等式(x-a)[x-(2-a)]<0的解集为N,若N⊆M,求a的取值范围.
分析 (1)若方程m=x2-x在[-1,1]上有解,即m的取值范围为函数y=x2-x在[-1,1]上的值域,结合二次函数的图象和性质,要得M;
(2)对a的取值进行分类讨论,求出不等式(x-a)[x-(2-a)]<0的解集为N,结合N⊆M,可得a的取值范围.
解答 解:(1)由题意知,方程m=x2-x在[-1,1]上有解,
即m的取值范围为函数y=x2-x在[-1,1]上的值域,
由函数y=x2-x的图象是开口朝上,且以直线x=$\frac{1}{2}$为对称轴的抛物线,
故当x=$\frac{1}{2}$时,函数最小值为-$\frac{1}{4}$,当x=-1时,函数最大值为2,
故m=[-$\frac{1}{4}$,2],(5分)
(2)当a=1时,解集N为空集,满足题意;(7分)
当a>1时,a>2-a,此时集合N={x|2-a<x<a},则1<a≤2(10分)
当a<1时,a<2-a,此时集合N={x|a<x<2-a},则-$\frac{1}{4}$≤a<1(13分)
综上:-$\frac{1}{4}$≤a≤2(14分)
点评 本题考查的知识点是集合的包含关系判断及应用,特称命题,是集合与逻辑的简单综合应用,难度不大,属于基础题.

练习册系列答案
相关题目
9.下表为某班5位同学身高x(单位:cm)与体重y(单位kg)的数据,
若两个量间的回归直线方程为$\widehat{y}$=1.16x+a,则a的值为( )
| 身高 | 170 | 171 | 166 | 178 | 160 |
| 体重 | 75 | 80 | 70 | 85 | 65 |
| A. | -122.2 | B. | -121.04 | C. | -91 | D. | -92.3 |
16.a=$\frac{1}{2}$cos6°-$\frac{\sqrt{3}}{2}$sin6°,b=2sin13°cos13°,c=$\sqrt{\frac{1-cos50°}{2}}$,则( )
| A. | a<c<b | B. | a<b<c | C. | a>b>c | D. | b<c<a |
13.已知“x>k”是“$\frac{2-x}{x+1}$<0”的充分不必要条件,则k的取值范围是( )
| A. | [2,+∞) | B. | [1,+∞) | C. | (-1,+∞) | D. | (-∞,-1] |
14.观察两个变量(存在线性相关关系)得如下数据:
则两变量间的线性回归方程为( )
| x | -10 | -6.99 | -5.01 | -2.98 | 3.98 | 5 | 7.99 | 8.01 |
| y | -9 | -7 | -5 | -3 | 4.01 | 4.99 | 7 | 8 |
| A. | $\hat y$=$\frac{1}{2}$x+1 | B. | $\hat y$=x | C. | $\hat y$=2x+$\frac{1}{3}$ | D. | $\hat y$=x+1 |
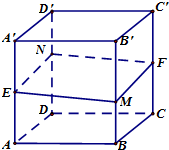 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′、DD′分别交于M,N两点,设BM=x,x∈[0,1],给出以下四个结论:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′、DD′分别交于M,N两点,设BM=x,x∈[0,1],给出以下四个结论: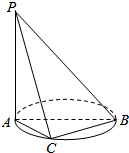 如图,AB是⊙O的直径,点C是⊙O上的动点,PA垂直于⊙O所在的平面.
如图,AB是⊙O的直径,点C是⊙O上的动点,PA垂直于⊙O所在的平面.