题目内容
【题目】在极坐标系中，设直线过点A（ 
， 
），B（3， 
），且直线与曲线C：ρ=2rsinθ（r＞0）有且只有一个公共点，求实数r的值．
【答案】解：点A（ 
， 
），B（3， 
），分别化为直角坐标A 
，B 
，即A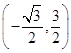 
，B（0，3）．
∴直线AB的方程为：y=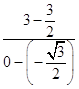 
x+3，化为：y= 
+3．
直线与曲线C：ρ=2rsinθ（r＞0）化为：ρ2=2rρsinθ，可得直角坐标方程：x2+y2=2ry，配方为：x2+（y﹣r）2=r2 ， 可得圆心C（0，r），半径r．
∵直线与曲线C：ρ=2rsinθ（r＞0）有且只有一个公共点，
∴直线与圆C相切，∴ 
=r，解得r=1
【解析】把极坐标及其极坐标方程化为直角坐标方程，利用直线与圆相切的充要条件即可得出．
练习册系列答案
阅读快车系列答案
相关题目
【题目】在某次试验中，两个试验数据x，y的统计结果如下面的表格1所示．
x | 1 | 2 | 3 | 4 | 5 |
y | 2 | 3 | 4 | 4 | 5 |
表格1
(1)在给出的坐标系中画出数据x，y的散点图．
(2)补全表格2，根据表格2中的数据和公式
求下列问题．
①求出y关于x的回归直线方程
中的
.
②估计当x＝10时，
的值是多少？
表格2
序号 | x | y | x2 | xy |
1 | 1 | 2 | 1 | 2 |
2 | 2 | 3 | 4 | 6 |
3 | 3 | 4 | 9 | 12 |
4 | 4 | 4 | 16 | 16 |
5 | 5 | 5 | 25 | 25 |
∑ |
