题目内容
(本题满分16分)设![]() ,
,![]()
(1)令![]() ,讨论
,讨论![]() 在(0.+∞)内的单调性并求极值;
在(0.+∞)内的单调性并求极值;
(2)求证:当![]() 时,恒有
时,恒有![]() 。
。
(1)![]() 在
在![]() 内是减函数,在
内是减函数,在![]() 内是增函数,
内是增函数, ![]() 处取得极小值
处取得极小值![]() (2)同解析.
(2)同解析.
解析:
(1)根据求导法则有![]() , ………………………2分
, ………………………2分
故![]() ,
,
于是![]() , ……………………4分
, ……………………4分
列表如下:
|
|
| 2 |
|
|
|
| 0 |
|
|
|
| 极小值 |
|
故知![]() 在
在![]() 内是减函数,在
内是减函数,在![]() 内是增函数,所以在
内是增函数,所以在![]() 处取得极小值
处取得极小值![]() . ………………………8分
. ………………………8分
(Ⅱ)证明:由![]() 知,
知,![]() 的极小值
的极小值![]() .
.
于是由上表知,对一切![]() ,恒有
,恒有![]() . ………………………10分
. ………………………10分
从而当![]() 时,恒有
时,恒有![]() ,故
,故![]() 在
在![]() 内单调增加. …………………12分
内单调增加. …………………12分
所以当![]() 时,
时,![]() ,即
,即![]() .
.
故当![]() 时,恒有
时,恒有![]() . …………………16分
. …………………16分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的前n项和为
的前n项和为 ,其中
,其中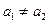 .
. 是数列
是数列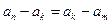 的任意项.
的任意项. ;
; 也成等差数列,且
也成等差数列,且 ,求数列
,求数列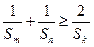 .
. 是圆心在抛物线
是圆心在抛物线 上的一系列圆,它们的圆心的横坐标分别记为
上的一系列圆,它们的圆心的横坐标分别记为 ,已知
,已知 ,又
,又
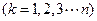 都与
都与 轴相切,且顺次逐个相邻外切. WWW.K**S*858$$U.COM
轴相切,且顺次逐个相邻外切. WWW.K**S*858$$U.COM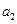 ;
; 的通项公式;
的通项公式; .
. 满足
满足 ,令
,令 .
. 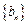 是否为等差数列?并说明理由;
是否为等差数列?并说明理由; ,求
,求 前
前 项的和
项的和 ;
; 使得
使得 三数成等比数列?
三数成等比数列? 的左,右两个焦点分别为
的左,右两个焦点分别为 ,短轴的上端点为
,短轴的上端点为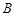 ,短轴上的两个三等分点为
,短轴上的两个三等分点为 ,且
,且 为正方形。
为正方形。 轴上的一个截距为
轴上的一个截距为 ,求此椭圆方程。
,求此椭圆方程。
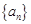 的前
的前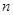 项和为
项和为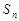 ,若对任意
,若对任意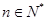 ,都有
,都有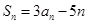 .
.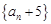 是等比数列,并求数列
是等比数列,并求数列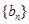 满足
满足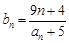 ,问是否存在
,问是否存在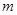 ,使得
,使得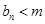 恒成立?如果存在,求出
恒成立?如果存在,求出