题目内容
(本题满分16分)
设数列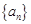 的前
的前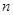 项和为
项和为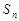 ,若对任意
,若对任意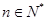 ,都有
,都有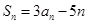 .
.
⑴求数列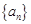 的首项;
的首项;
⑵求证:数列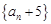 是等比数列,并求数列
是等比数列,并求数列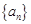 的通项公式;
的通项公式;
⑶数列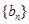 满足
满足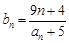 ,问是否存在
,问是否存在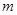 ,使得
,使得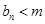 恒成立?如果存在,求出
恒成立?如果存在,求出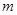 的值,如果不存在,说明理由.
的值,如果不存在,说明理由.
【答案】
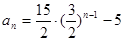 ,
,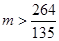
【解析】解:[来源:Z.xx.k.Com]
⑴∵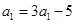 ∴
∴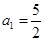 ……………………………3分
……………………………3分
⑵∵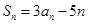 ∴
∴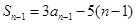 (
(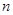 ≥2)
≥2)
∴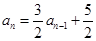 ………………………………5分
………………………………5分
∴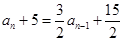
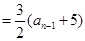
∴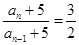 (为常数)
(
(为常数)
(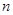 ≥2)
≥2)
∴数列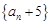 是以
是以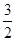 为公比的等比数列
…………………………………7分
为公比的等比数列
…………………………………7分
∴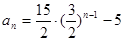 …………………………………10分
…………………………………10分
⑶∵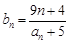 ∴
∴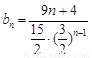
∴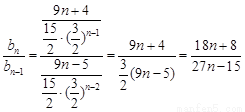 ………………………………12分
………………………………12分
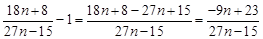 ………………………………14分
………………………………14分
∴当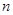 ≥3时,
≥3时,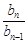 <1;
当
<1;
当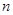 =2时,
=2时,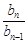 >1
>1
∴当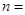 2时,
2时,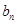 有最大值
有最大值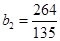
∴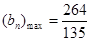 …………………………………15分
…………………………………15分
∴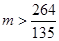 …………………………………16分
…………………………………16分

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目


 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在