题目内容
(本题满分16分)设椭圆 的左,右两个焦点分别为
的左,右两个焦点分别为 ,短轴的上端点为
,短轴的上端点为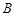 ,短轴上的两个三等分点为
,短轴上的两个三等分点为 ,且
,且 为正方形。
为正方形。
(1)求椭圆的离心率;
(2)若过点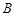 作此正方形的外接圆的切线在
作此正方形的外接圆的切线在 轴上的一个截距为
轴上的一个截距为 ,求此椭圆方程。
,求此椭圆方程。

【答案】
(1)由题意知: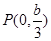 ,设
,设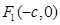 ……………………………… 2分
……………………………… 2分
因为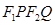 为正方形,所以
为正方形,所以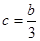 ……………………………………… 4分
……………………………………… 4分
即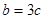 ,∴
,∴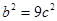 ,即
,即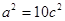 ,所以离心率
,所以离心率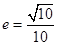 ………… 6分
………… 6分
(2)因为B(0,3c),由几何关系可求得一条切线的斜率为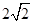 ………… 10分
………… 10分
所以切线方程为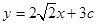 ,……………………………………………… 12分
,……………………………………………… 12分
因为在轴上的截距为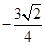 ,所以
,所以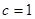 ,……………………………………… 14分
,……………………………………… 14分
所求椭圆方程为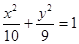 ……………………………………………………… 16分
……………………………………………………… 16分
【解析】略

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
 的前n项和为
的前n项和为 ,其中
,其中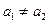 .
. 是数列
是数列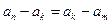 的任意项.
的任意项. ;
; 也成等差数列,且
也成等差数列,且 ,求数列
,求数列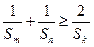 .
. 是圆心在抛物线
是圆心在抛物线 上的一系列圆,它们的圆心的横坐标分别记为
上的一系列圆,它们的圆心的横坐标分别记为 ,已知
,已知 ,又
,又
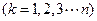 都与
都与 轴相切,且顺次逐个相邻外切. WWW.K**S*858$$U.COM
轴相切,且顺次逐个相邻外切. WWW.K**S*858$$U.COM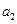 ;
; 的通项公式;
的通项公式; .
. 满足
满足 ,令
,令 .
. 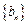 是否为等差数列?并说明理由;
是否为等差数列?并说明理由; ,求
,求 前
前 项的和
项的和 ;
; 使得
使得 三数成等比数列?
三数成等比数列?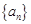 的前
的前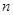 项和为
项和为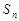 ,若对任意
,若对任意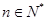 ,都有
,都有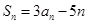 .
.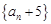 是等比数列,并求数列
是等比数列,并求数列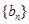 满足
满足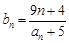 ,问是否存在
,问是否存在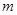 ,使得
,使得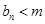 恒成立?如果存在,求出
恒成立?如果存在,求出