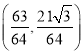ЬтФПФкШн
ЁОЬтФПЁПФГФІЭаГЕЩњВњЦѓвЕЃЌЩЯФъЖШЩњВњФІЭаГЕЕФЭЖШыГЩБОЮЊ1ЭђдЊ/СОЃЌГіГЇМлЮЊ1.2ЭђдЊ/СОЃЌФъЯњЪлСПЮЊ1000СОЃЎБОФъЖШЮЊЪЪгІЪаГЁашЧѓЃЌМЦЛЎЬсИпВњЦЗЕЕДЮЃЌЪЪЖШдіМгЭЖШыГЩБОЃЎШєУПСОГЕЭЖШыГЩБОдіМгЕФБШР§ЮЊxЃЈ0ЃМxЃМ1ЃЉЃЌдђГіГЇМлЯргІЕФЬсИпБШР§ЮЊ0.75xЃЌЭЌЪБдЄМЦФъЯњЪлСПдіМгЕФБШР§ЮЊ0.6xЃЎвбжЊФъРћШѓ=ЃЈГіГЇМлЉЭЖШыГЩБОЃЉЁСФъЯњЪлСПЃЎ
ЃЈ1ЃЉаДГіБОФъЖШдЄМЦЕФФъРћШѓyгыЭЖШыГЩБОдіМгЕФБШР§xЕФЙиЯЕЪНЃЛ
ЃЈ2ЃЉЮЊЪЙБОФъЖШЕФФъРћШѓБШЩЯФъгаЫљдіМгЃЌЮЪЭЖШыГЩБОдіМгЕФБШР§xгІдкЪВУДЗЖЮЇФкЃП
ЁОД№АИЁПЃЈ1ЃЉy=Љ60x2+20x+200ЃЈ0ЃМxЃМ1ЃЉЃЎЃЈ2ЃЉЮЊБЃжЄБОФъЖШЕФФъРћШѓБШЩЯФъЖШгаЫљдіМгЃЌЭЖШыГЩБОдіМгЕФБШР§xгІТњзу 0ЃМxЃМ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉИљОнШєУПСОГЕЭЖШыГЩБОдіМгЕФБШР§ЮЊxЃЈ0ЃМxЃМ1ЃЉЃЌдђГіГЇМлЯргІЕФЬсИпБШР§ЮЊ0.75xЃЌЭЌЪБдЄМЦФъЯњЪлСПдіМгЕФБШР§ЮЊ0.6xКЭФъРћШѓ=ЃЈГіГЇМлЉЭЖШыГЩБОЃЉЁСФъЯњЪлСПЃЎНЈСЂРћШѓФЃаЭЃЌвЊзЂвтЖЈвхгђЃЎ
ЃЈ2ЃЉвЊБЃжЄБОФъЖШЕФРћШѓБШЩЯФъЖШгаЫљдіМгЃЌжЛашНёФъЕФРћШѓМѕШЅЕФРћШѓДѓгкСуМДПЩЃЌНтВЛЕШЪНПЩЧѓЕУНсЙћЃЌвЊзЂвтБШР§ЕФЗЖЮЇЃЎ
НтЃКЃЈ1ЃЉгЩЬтвтЕУ
y=[1.2ЁСЃЈ1+0.75xЃЉЉ1ЁСЃЈ1+xЃЉ]ЁС1000ЁСЃЈ1+0.6xЃЉЃЈ0ЃМxЃМ1ЃЉЃЈ4ЗжЃЉ
ећРэЕУy=Љ60x2+20x+200ЃЈ0ЃМxЃМ1ЃЉЃЎЃЈ6ЗжЃЉ
ЃЈ2ЃЉвЊБЃжЄБОФъЖШЕФРћШѓБШЩЯФъЖШгаЫљдіМгЃЌЕБЧвНіЕБ![]()
МД![]() ЃЈ9ЗжЃЉ
ЃЈ9ЗжЃЉ
НтВЛЕШЪНЕУ![]() ЃЎ
ЃЎ
Д№ЃКЮЊБЃжЄБОФъЖШЕФФъРћШѓБШЩЯФъЖШгаЫљдіМгЃЌЭЖШыГЩБОдіМгЕФБШР§xгІТњзу 0ЃМxЃМ![]() ЃЎЃЈ12ЗжЃЉ
ЃЎЃЈ12ЗжЃЉ

 КЃЕэПЮЪБаТзївЕН№АёОэЯЕСаД№АИ
КЃЕэПЮЪБаТзївЕН№АёОэЯЕСаД№АИ ЦкФЉН№ХЦОэЯЕСаД№АИ
ЦкФЉН№ХЦОэЯЕСаД№АИ ЧсЫЩПЮЬУБъзМСЗЯЕСаД№АИ
ЧсЫЩПЮЬУБъзМСЗЯЕСаД№АИ