题目内容
【题目】在平面直角坐标系![]() 中,
中,![]() 是椭圆
是椭圆![]() :
:![]() 上的点,过点
上的点,过点![]() 的直线的方程为
的直线的方程为![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)当![]() 时,
时,
(i)设直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于
轴分别相交于![]() ,
,![]() 两点,求
两点,求![]() 的最小值;
的最小值;
(ii)设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,点
,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,求证:点
对称,求证:点![]() ,
,![]() ,
,![]() 三点共线.
三点共线.
【答案】(1)![]() (2)(i)
(2)(i)![]() (ii)证明见解析
(ii)证明见解析
【解析】
(1)由椭圆方程求出![]() 可得离心率;
可得离心率;
(2)(i)求出直线![]() 与坐标轴交点
与坐标轴交点![]() 的坐标,可得出
的坐标,可得出![]() 面积为
面积为![]() ,由
,由![]() 在椭圆上,可得
在椭圆上,可得![]() ,由基本不等式可得
,由基本不等式可得![]() 的最大值,从而得面积最小值;
的最大值,从而得面积最小值;
(ii)求出对称点![]() 的坐标,验证三点共线.可分类
的坐标,验证三点共线.可分类![]() 和
和![]() 分别求解.
分别求解.
(1)依题![]() ,
,![]() ,
,
所以椭圆![]() 离心率为
离心率为![]() .
.
(2)依题意![]() ,令
,令![]() ,由
,由![]() ,得
,得![]() ,则
,则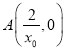 .
.
令![]() ,由
,由![]() ,得
,得![]() ,则
,则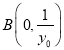 .
.
则![]() 的面积
的面积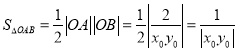 .
.
因为点![]() 在
在![]() 上,所以
上,所以![]() .
.
因为![]() ,即
,即![]() ,则
,则![]() .
.
所以![]() .
.
当且仅当![]() ,即
,即![]() ,
,![]() ,
,![]() 面积的最小值为
面积的最小值为![]() .
.
(3)由![]() ,解得
,解得![]() .
.
①当![]() 时,
时,![]() ,
,![]() ,此时
,此时![]() ,
,![]() .
.
因为![]() ,所以三点
,所以三点![]() ,
,![]() ,
,![]() 共线.
共线.
当![]() 时,也满足.
时,也满足.
②当![]() 时,设
时,设![]() ,
,![]() ,
,![]() 的中点为
的中点为![]() ,则
,则![]() ,代入直线
,代入直线![]() 的方程,得:
的方程,得:
![]() .
.
设直线![]() 的斜率为
的斜率为![]() ,则
,则![]() ,
,
所以![]() .
.
由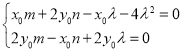 ,解得
,解得![]() ,
,![]() .
.
所以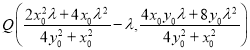 .
.
当点![]() 的横坐标与点
的横坐标与点![]() 的横坐标相等时,把
的横坐标相等时,把![]() ,
,![]() 代入
代入![]() 中得
中得![]() ,则
,则![]() ,
,![]() ,
,![]() 三点共线.
三点共线.
当点![]() 的横坐标与点
的横坐标与点![]() 的横坐标不相等时,
的横坐标不相等时,
直线![]() 的斜率为
的斜率为![]() .由
.由![]() ,
,![]() .
.
所以直线![]() 的斜率为
的斜率为
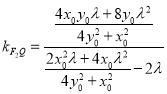
![]()
![]()
![]()
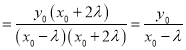 .
.
因为![]() ,所以
,所以![]() ,
,![]() ,
,![]() 三点共线,
三点共线,
综上所述![]() ,
,![]() ,
,![]() 三点共线.
三点共线.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案【题目】“互联网+”是“智慧城市”的重要内容,A市在智慧城市的建设中,为方便市民使用互联网,在主城区覆盖了免费WiFi为了解免费WiFi在A市的使用情况,调查机构借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到如下列联表(单位:人):
经常使用免费WiFi | 偶尔或不用免费WiFi | 合计 | |
45岁及以下 | 70 | 30 | 100 |
45岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,判断是否有90%的把握认为A市使用免费WiFi的情况与年龄有关;
(2)将频率视为概率,现从该市45岁以上的市民中用随机抽样的方法每次抽取1人,共抽取3次.记被抽取的3人中“偶尔或不用免费WiFi”的人数为X,若每次抽取的结果是相互独立的,求X的分布列,数学期望E(X)和方差D(X).附:![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |