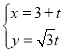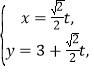题目内容
【题目】在直角坐标系![]() 中,已知定点
中,已知定点![]() 、
、![]() ,动点
,动点![]() 满足
满足![]() ,设点
,设点![]() 的曲线为
的曲线为![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() 两点.
两点.![]()
(1)写出曲线![]() 的方程,并指出曲线
的方程,并指出曲线![]() 的轨迹;
的轨迹;
(2)当![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)证明:存在直线![]() ,满足
,满足![]() ,并求实数
,并求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,曲线
,曲线![]() 的轨迹是以
的轨迹是以![]() 、
、![]() 为焦点的双曲线的上支;(2)
为焦点的双曲线的上支;(2)![]() 或
或![]() ;(3)详见解析,
;(3)详见解析,![]() ,
,![]()
【解析】
(1)结合双曲线的定义,可知点![]() 的轨迹是以
的轨迹是以![]() 、
、![]() 为焦点的双曲线的上支,求出轨迹方程即可;
为焦点的双曲线的上支,求出轨迹方程即可;
(2)将直线与![]() 的方程联立,消去
的方程联立,消去![]() ,可得到关于
,可得到关于![]() 的一元二次方程,令
的一元二次方程,令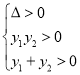 ,求解即可;
,求解即可;
(3)联立直线与![]() 的方程,得到关于
的方程,得到关于![]() 的一元二次方程,由
的一元二次方程,由![]() ,可得
,可得![]() ,设
,设![]() ,则
,则![]() ,结合根与系数关系,可得到
,结合根与系数关系,可得到![]() ,若存在符合题意的直线,还需要满足以下三个条件:①
,若存在符合题意的直线,还需要满足以下三个条件:①![]() ;②
;②![]() ;③
;③![]() ,求解即可.
,求解即可.
(1)动点![]() 满足
满足![]() ,且
,且![]() 、
、![]() ,所以点
,所以点![]() 的轨迹是以
的轨迹是以![]() 、
、![]() 为焦点的双曲线的上支,
为焦点的双曲线的上支,![]() ,
,![]() ,
,![]() ,
,
所以曲线![]() 的方程为
的方程为![]() ;
;
(2)由题意,联立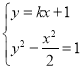 ,消去
,消去![]() ,得
,得![]() ,
,
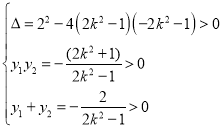 ,解得
,解得![]() 或
或![]() .
.
故![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.
(3)因为![]() ,所以
,所以![]() ,设
,设![]() ,则
,则![]() .
.
联立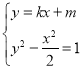 ,可得
,可得![]() ,
,![]() ,
,
则![]()
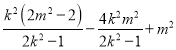
![]() ,
,![]() ,
,
所以![]() ,整理得
,整理得![]() .
.
若存在符合题意的直线,还需要满足以下三个条件:①![]() ;②
;②![]() ;③
;③![]() .
.
①![]() ,整理得
,整理得![]() ,又
,又![]() ,则
,则![]() ,显然恒成立;
,显然恒成立;
②![]() ,等价于
,等价于![]() ,
,
因为![]() 恒成立,所以
恒成立,所以![]() ,即
,即![]() ;
;
③![]() ,由②知
,由②知![]() ,所以
,所以![]() .
.
所以![]() 满足
满足![]() ,即
,即![]() .
.
又因为![]() ,所以
,所以![]() ,且
,且![]() ,故
,故![]() .
.
所以存在直线![]() ,满足
,满足![]() ,
,![]() 的取值范围为:
的取值范围为:![]() ,
,![]() 的取值范围为:
的取值范围为:![]() .
.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).
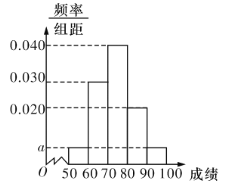
(1)求图中![]() 的值;
的值;
(2)根据已知条件完成下面![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“晋级成功”与性别有关?
的把握认为“晋级成功”与性别有关?
晋级成功 | 晋级失败 | 合计 | |
男 | 16 | ||
女 | 50 | ||
合计 |
(参考公式: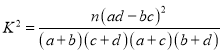 ,其中
,其中![]() )
)
| 0.40 | 0.025 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
(3)将频率视为概率,从本次考试80分以上的所有人员中,按分层抽样的方式抽取5个人的样本;现从5人样本中随机选取2人,求选取的2人恰好都来自区间![]() 的概率.
的概率.