题目内容
12.已知集合A={a-2,12,2a2+5a},且-3∈A,求a的值.分析 由∵-3∈A得:a-2=-3,或2a2+5a=-3,解出a值,利用集合元素的互异性检验,可得答案.
解答 解:∵-3∈A,
∴a-2=-3,或2a2+5a=-3,
得:a=-1,或a=-$\frac{3}{2}$,
检验知:a=-1不满足集合元素的互异性,
∴a=-$\frac{3}{2}$.
点评 本题考查的知识点是元素与集合的关系,集合元素的互异性,难度不大,属于基础题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
17.函数y=$\sqrt{\frac{1}{4}-si{n}^{2}x}$+|sinx|的值域是( )
| A. | [-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$] | B. | [0,$\frac{\sqrt{2}}{2}$] | C. | [0,$\frac{\sqrt{3}}{2}$] | D. | [$\frac{1}{2}$,$\frac{\sqrt{2}}{2}$] |
4.命题p:?x∈R,x2+ax+a2≥0;命题q:若一条直线不在平面内,则这条直线就与这个平面平行,则下列命题中为真命题的是( )
| A. | p∨q | B. | p∧q | C. | (¬p)∨q | D. | (¬p)∧(¬q) |
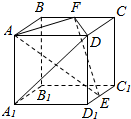 如图所示,在正方体ABCD-A1B1C1D1中,E为棱C1D1的中点,F为棱BC的中点.求证:直线AE⊥直线DA1.
如图所示,在正方体ABCD-A1B1C1D1中,E为棱C1D1的中点,F为棱BC的中点.求证:直线AE⊥直线DA1.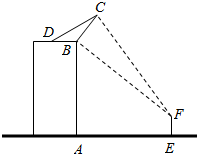 如图,一楼房高AB为19$\sqrt{3}$米,某广告公司在楼顶安装一块宽BC为4米的广告牌,CD为拉杆,广告牌的倾角为60°,安装过程中,一身高为$\sqrt{3}$米的监理人员EF站在楼前观察该广传牌的安装效果:为保证安全,该监理人员不得站在广告牌的正下方:设AE=x米,该监理人员观察广告牌的视角∠BFC=θ.
如图,一楼房高AB为19$\sqrt{3}$米,某广告公司在楼顶安装一块宽BC为4米的广告牌,CD为拉杆,广告牌的倾角为60°,安装过程中,一身高为$\sqrt{3}$米的监理人员EF站在楼前观察该广传牌的安装效果:为保证安全,该监理人员不得站在广告牌的正下方:设AE=x米,该监理人员观察广告牌的视角∠BFC=θ.