题目内容
【题目】在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,侧面
,侧面![]() 是边长为
是边长为![]() 的等边三角形,底面
的等边三角形,底面![]() 是矩形,且
是矩形,且![]() ,则该四棱锥外接球的表面积等于__________.
,则该四棱锥外接球的表面积等于__________.
【答案】![]()
【解析】∵平面SAB⊥平面SAD,平面SAB∩平面SAD=SA,侧面SAB是边长为![]() 的等边三角形,设AB的中点为E,SA的中点为F,
的等边三角形,设AB的中点为E,SA的中点为F,
则BF⊥SA,∴BF⊥平面SAD,∴BF⊥AD,底面ABCD是矩形,∴AD⊥平面SAB,SE平面SAB,
∴AD⊥SE,又SE⊥AB,AB∩AD=A,
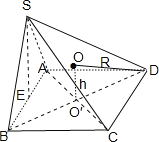
∴SE⊥底面ABCD,作图如下:
∵SAB是边长为![]() 的等边三角形,
的等边三角形,
∴![]() .
.
又底面ABCD是矩形,且BC=4,
∴矩形ABCD的对角线长为![]() ,
,
∴矩形ABCD的外接圆的半径为![]() .
.
设该四棱锥外接球的球心为O,半径为R,O到底面的距离为h,
则r2+h2=R2,即7+h2=R2,又R2=22+(SEh)2=4+(3h)2,
∴7+h2=4+(3h)2,
∴h=1.
∴R2=7+h2=8,
∴该四棱锥外接球的表面积![]() .
.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目