题目内容
【题目】已知椭圆
的离心率为
，且过点
（Ⅰ）求椭圆
的方程；
（Ⅱ）设直线
与圆
相切于点
，且
与椭圆
只有一个公共点
.
①求证： 
；
②当
为何值时， 
取得最大值？并求出最大值.
【答案】(Ⅰ) 
；(Ⅱ)①.证明见解析；②.答案见解析.
【解析】试题分析：(1)椭圆的离心率为
，又椭圆过已知点，即
，再加上
，联立可求得
；（2）直线与圆及椭圆都相切，因此可以把直线方程与椭圆方程(或圆方程)联立方程组，此方程组只有一解，由此可得到题中参数的关系式，当然直线与圆相切，可利用圆心到直线的距离等于圆的半径来列式，得到的两个等式中消去参数
即可证得①式；而②要求
的最大值，可先求出
，注意到
，因此
，这里设
，由①中的方程(组)可求得
，最终把
用
表示， 
，利用不等式知识就可求得最大值.
试题解析：(1)椭圆E的方程为
4分
（2）①因为直线
与圆C: 
相切于A,得
,
即
① 5分
又因为
与椭圆E只有一个公共点B，
由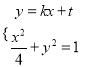
得
,且此方程有唯一解.
则
即
②由①②,得
8分
②设
，由
得
由韦达定理, 
∵
点在椭圆上,∴
∴
10分
在直角三角形OAB中, 
∴
12分
练习册系列答案
相关题目
