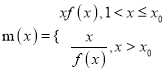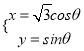题目内容
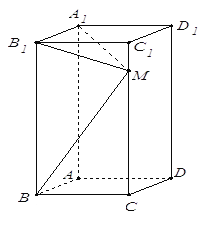
【题目】如图所示，在长方体
中， 
， 
， 
， 
为棱
上一点，
（1）若
，求异面直线
和
所成角的正切值；
（2）若
，求证
平面
.
【答案】（1）
（2）见解析
【解析】试题分析：（1）线线角找平行，因为
，所以
（或其补角）是异面直线
和
所成角，解三角形可得
（2）先根据勾股数得
，再结合
面
可得
，最后根据线面垂直判定定理可得
平面
.
试题解析：解:（1）
，所以
（或其补角）是异面直线
和
所成角
长方体
中 
面
，
， 
， 
，得
（2）由题意， 
， 
， 
， 
，即
又由
面
可得
故
平面
.
点睛:垂直、平行关系证明中应用转化与化归思想的常见类型.
(1)证明线面、面面平行，需转化为证明线线平行.
(2)证明线面垂直，需转化为证明线线垂直.
(3)证明线线垂直，需转化为证明线面垂直.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某市对贫困家庭自主创业给予小额贷款补贴，每户贷款额为
万元，贷款期限有
个月、
个月、
个月、
个月、
个月五种，这五种贷款期限政府分别需要补助
元、
元、
元、
元、
元，从
年享受此项政策的困难户中抽取了
户进行了调查统计，选取贷款期限的频数如下表：
贷款期限 |
|
|
|
|
|
频数 |
|
|
|
|
|
以商标各种贷款期限的频率作为
年贫困家庭选择各种贷款期限的概率.
（1）某小区
年共有
户准备享受此项政策，计算其中恰有两户选择贷款期限为
个月的概率；
（2）设给享受此项政策的某困难户补贴为
元，写出
的分布列，若预计
年全市有
万户享受此项政策，估计
年该市共要补贴多少万元.
