题目内容
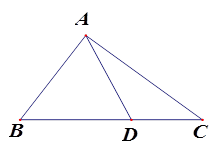
如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上,此时到达C处.
(1)求渔船甲的速度;
(2)求sinα的值.
(1)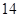 海里/小时;(2)
海里/小时;(2)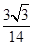 .
.
解析试题分析:(1)首先利用余弦定理求出BC,即可求出渔船甲的速度;
(2)由余弦定理求出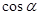 ,再利用同角及泵西求出
,再利用同角及泵西求出 .
.
试题解析:解:(1)依题意, ,
, ,
,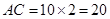 ,
, .
.
在△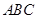 中,由余弦定理,得
中,由余弦定理,得
 .解得
.解得 . 4分
. 4分
所以渔船甲的速度为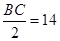 海里/小时.
海里/小时.
答:渔船甲的速度为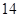 海里/小时. 6分
海里/小时. 6分
(2)在△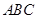 中,因为
中,因为 ,
, ,
, ,
, ,
,
由余弦定理,得 .即
.即 . 9分
. 9分
因为 为锐角,所以
为锐角,所以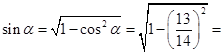
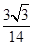 .
.
答: 的值为
的值为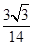 . 12分
. 12分
法二:在△ABC中,因为AB=12(海里),∠BAC=120°,BC=28(海里),∠BCA=α,由正弦定理,得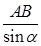 =
= .
.
即sinα=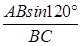 =
= =
=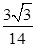 . 11分
. 11分
答: 的值为
的值为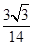 . 12分
. 12分
考点:1.正弦定理和余弦定理;2.同角的基本关系.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 cos4x (1)求f(x)的最小正周期及最大值。
cos4x (1)求f(x)的最小正周期及最大值。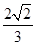 ,f(
,f(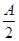 )=-
)=-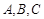 所对的边分别为
所对的边分别为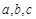 ,已知
,已知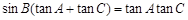 .
. ,求△
,求△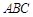 的面积S.
的面积S.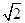 ,b=
,b=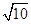 ,求c;
,求c;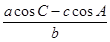 的取值范围.
的取值范围.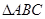 中,角
中,角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、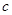 .已知
.已知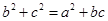 .
.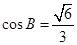 ,
,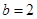 ,求
,求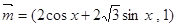 ,
, ,且
,且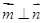 .
.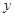 表示为
表示为 的函数
的函数 ,并求
,并求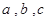 分别为
分别为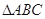 的三个内角
的三个内角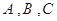 对应的边长,若
对应的边长,若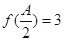 ,且
,且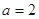 ,
,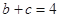 ,求
,求 中,角
中,角 的对边分别为
的对边分别为 ,且
,且 .
.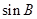 的值;
的值; 的值.
的值.