题目内容
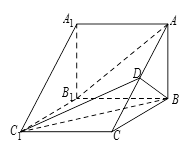
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点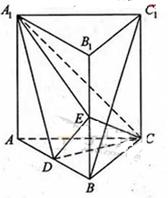
(Ⅰ)证明:BC1//平面A1CD;
(Ⅱ)设AA1=AC=CB=2,AB=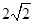 ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
(Ⅰ)详见解析;(Ⅱ)三棱锥C一A1DE的体积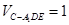 .
.
解析试题分析:(Ⅰ)证明:BC1//平面A1CD,证明线面平行,首先证明线线平行,可用三角形的中位线平行,也可用平行四边形的对边平行,注意到D,分别是AB,的中点,可考虑利用三角形的中位线平行,连结 交
交 于点F,则F为
于点F,则F为 中点,连结DF,则
中点,连结DF,则 ∥DF,从而可证;(Ⅱ)求三棱锥C一A1DE的体积.求体积,关键是找高,由已知
∥DF,从而可证;(Ⅱ)求三棱锥C一A1DE的体积.求体积,关键是找高,由已知 =2,
=2,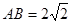 ,可知三角形
,可知三角形 是等腰直角三角形,又因为
是等腰直角三角形,又因为 是直三棱柱,则
是直三棱柱,则 ,
, 即为高,有平面几何知识可得
即为高,有平面几何知识可得 是直角三角形,可求得面积,从而可得体积.
是直角三角形,可求得面积,从而可得体积.
试题解析:(Ⅰ)连结 交
交 于点F,则F为
于点F,则F为 中点,又D是AB中点,连结DF,则
中点,又D是AB中点,连结DF,则 ∥DF
∥DF
因为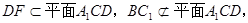 所以
所以 ∥平面
∥平面
(Ⅱ)因为 是直三棱柱,所以,
是直三棱柱,所以,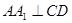 ,由已知AC=CB,D为AB的中点,所以
,由已知AC=CB,D为AB的中点,所以 ,又
,又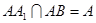 ,于是
,于是 .由
.由 =2,
=2,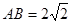 得
得 ,
,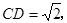
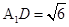 ,
,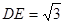 ,
,
 E=3,
E=3,
故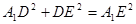 ,
,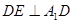 ,所以
,所以 (12分)
(12分)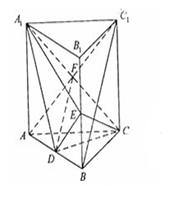
考点:线面平行的判定,几何体的体积.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
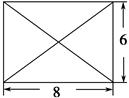
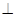 平面ABCD,四边形ABCD为矩形,PA=AB=
平面ABCD,四边形ABCD为矩形,PA=AB= ,AD=1,点F是PB的中点,点E在边BC上移动.
,AD=1,点F是PB的中点,点E在边BC上移动.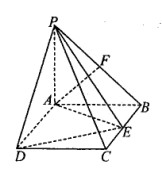
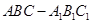 中,侧棱
中,侧棱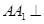 底面
底面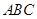 ,
,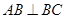 ,
,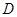 为
为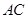 的中点,
的中点,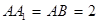 .
.
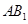 //平面
//平面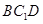 ;
;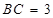 ,求四棱锥
,求四棱锥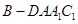 的体积.
的体积. 中,侧棱长均为
中,侧棱长均为 ,底边
,底边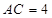 ,
, ,
, ,
,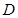 、
、 分别为
分别为 、
、 的中点.
的中点.
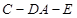 的平面角.
的平面角.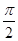 .
.
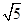 ,求三棱锥C1-ABA1的体积.
,求三棱锥C1-ABA1的体积.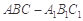 中,侧棱与底面垂直,
中,侧棱与底面垂直,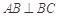 ,
,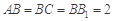 ,
,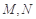 分别是
分别是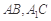 的中点
的中点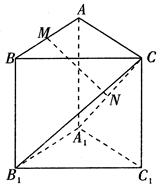
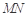 ∥平面
∥平面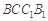 ;
;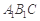 ;
;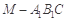 的体积.
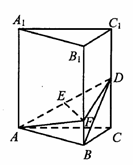
的体积. 中,
中,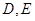 分别为
分别为 、
、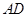 的中点,
的中点, 为
为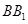 上的点,且
上的点,且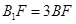
 ∥平面
∥平面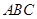 ;
;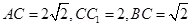 ,
, ,求三棱锥
,求三棱锥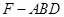 的体积.
的体积. 的三视图如图所示.
的三视图如图所示.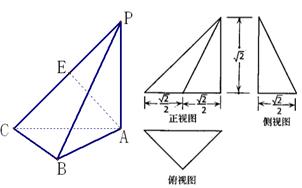
 是直角三角形;
是直角三角形; 求三棱锥
求三棱锥 在线段
在线段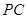 上何处时,
上何处时,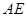 与平面
与平面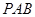 所成的角为
所成的角为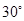 .
.