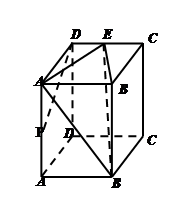题目内容
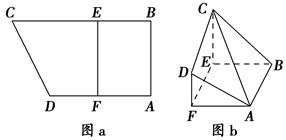
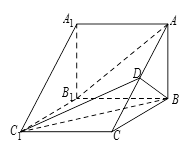
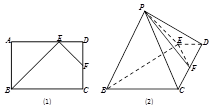
已知梯形ABCD中,AD∥BC,∠ABC =∠BAD =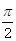 ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .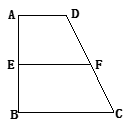
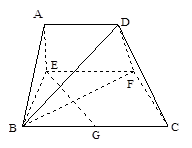
(1) 当x=2时,求证:BD⊥EG ;
(2) 若以F、B、C、D为顶点的三棱锥的体积记为f(x),求f(x)的最大值;
(3) 当f(x)取得最大值时,求二面角D-BF-C的余弦值.
(1)参考解析;(2)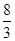 ;-
;-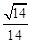
解析试题分析:(1)通过建立空间直角坐标系.写出相应的坐标,再写出BD向量和EG向量.从而计算这两向量的数量积.即可得两直线垂直.本小题也可以通过转化为线面垂直来证明.
(2)以F、B、C、D为顶点的三棱锥的体积是以三角形BFC为底面,三棱锥的高为x.由三棱锥体积可得f(x).在通过求二次函数的最值即可结论.
(3)由(2)可得x=2.求二面角关键是求出两个平面的法向量.由于平面BFC的法向量可以是向量EA.另外平面DBF的法向量要通过法向量的计算方法可求得.再由两法向量求出向量夹角的余弦值.再通过图形的判断二面角的大小来判断是钝角还是锐角在确定余弦值的正负.本小题也可以作出二面角的平面角.通过计算求得余弦值.
试题解析:(1)(法一)∵平面 平面
平面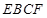 ,AE⊥EF,∴AE⊥面平面
,AE⊥EF,∴AE⊥面平面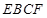 ,AE⊥EF,AE⊥BE,又BE⊥EF,故可如图建立空间坐标系E-xyz。 1分
,AE⊥EF,AE⊥BE,又BE⊥EF,故可如图建立空间坐标系E-xyz。 1分
则A(0,0,2),B(2,0,0),G(2,2,0),D(0,2,2),E(0,0,0) 2分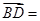 (-2,2,2),
(-2,2,2),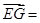 (2,2,0) 3分
(2,2,0) 3分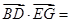 (-2,2,2)
(-2,2,2)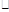 (2,2,0)=0,∴
(2,2,0)=0,∴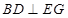 4分
4分
(法二)作DH⊥EF于H,连BH,GH, 1分
由平面 平面
平面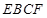 知:DH⊥平面EBCF,
知:DH⊥平面EBCF,
而EG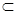 平面EBCF,故EG⊥DH。
平面EBCF,故EG⊥DH。
又四边形BGHE为正方形,∴EG⊥BH,
BH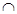 DH=H,故EG⊥平面DBH, 3分
DH=H,故EG⊥平面DBH, 3分
而BD 平面DBH,∴ EG⊥BD。 4分
平面DBH,∴ EG⊥BD。 4分
(或者直接利用三垂线定理得出结果)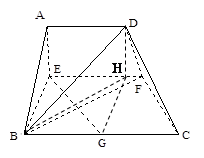
(2)∵AD∥面BFC,
所以 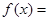 VA-BFC=
VA-BFC=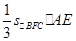 =
=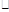
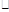 4
4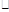 (4-x)
(4-x)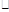 x
x 7分
7分
即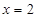 时
时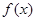 有最大值为
有最大值为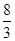 . 8分
. 8分
(3)(法一)设平面DBF的法向量为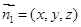 ,∵AE="2," B(2,0,0),D(0,2,2),
,∵AE="2," B(2,0,0),D(0,2,2),
F(0,3,0),∴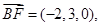
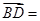 (-2,2,2), 9分
(-2,2,2), 9分
则 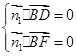 ,
,
即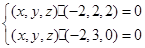 ,
,
取x=3,则y=2,z=1,∴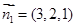
面BCF的一个法向量为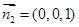 12分
12分
则cos<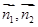 >=
>=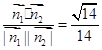 14分
14分
由于所求二面角D-BF-C的平面角为钝角,所以此二面角的余弦值为-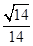
(法二)作DH⊥EF于H,作HM⊥BF,连DM。
由三垂线定理知 BF⊥DM,∴∠DMH是二面角D-BF-C的平面角的补角。 9分
由△HMF∽△EBF,知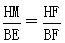 ,而HF=1,BE=2,
,而HF=1,BE=2,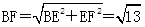 ,∴HM=
,∴HM=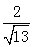 。
。
又DH=2,
∴在Rt△HMD中,tan∠DMH=- ,
,
因∠DMH为锐角,∴cos∠DMH=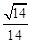 , 13分
, 13分
而∠DMH是二面角D-BF-C的平面角的补角,
故二面角D-BF-C的余弦值为-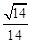 .
.
考点:1.线线垂直.2.体积问题.3.二面角求解.4.空间坐标系解决立几知识.5.立几中纯推理的应用.

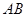 和AB1的中点,点F在BC上且满足BF∶FC=1∶3.
和AB1的中点,点F在BC上且满足BF∶FC=1∶3.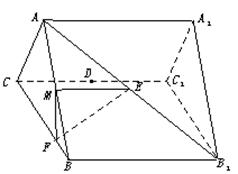
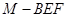 的体积.
的体积.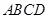 的对角线交于点G,AD⊥平面
的对角线交于点G,AD⊥平面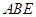 ,
, ,
, ,
,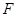 为
为 上的点,且BF⊥平面ACE
上的点,且BF⊥平面ACE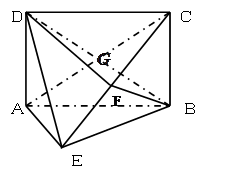
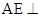 平面
平面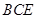 ;
;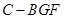 的体积.
的体积.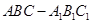 中,侧棱
中,侧棱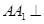 底面
底面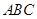 ,
,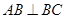 ,
,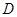 为
为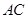 的中点,
的中点,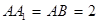 .
.
 //平面
//平面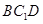 ;
;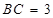 ,求四棱锥
,求四棱锥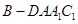 的体积.
的体积.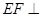 平面
平面 ,
, ,
,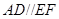 ,
,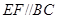 ,
,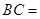
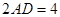 ,
,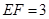 ,
,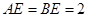 ,
, 是
是 的中点.
的中点.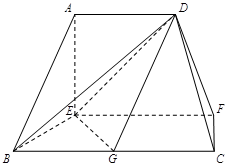
 平面
平面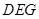 ;
;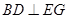 ;
;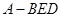 的体积.
的体积.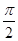 .
.
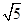 ,求三棱锥C1-ABA1的体积.
,求三棱锥C1-ABA1的体积.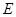 是矩形
是矩形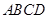 中
中 边上的点,
边上的点,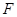 为
为 边的中点,
边的中点,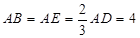 ,现将
,现将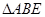 沿
沿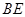 边折至
边折至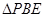 位置,且平面
位置,且平面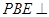 平面
平面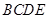 .
.
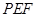 ;
;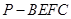 的体积.
的体积. 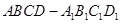 中,棱长为2,
中,棱长为2, 是棱
是棱 上中点,
上中点,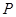 是棱
是棱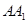 中点,(1)求证:
中点,(1)求证: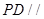 面
面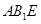 ;(2)求三棱锥
;(2)求三棱锥 的体积.
的体积.