题目内容
我们把焦点相同,且离心率互为倒数的椭圆和双曲线称为一对“相关曲线”.已知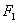 、
、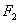 是一对相关曲线的焦点,
是一对相关曲线的焦点,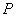 是它们在第一象限的交点,当
是它们在第一象限的交点,当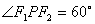 时,这一对相关曲线中双曲线的离心率是( )
时,这一对相关曲线中双曲线的离心率是( )
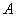 .
.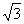
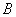 .
.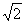
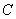 .
.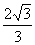
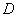 .
.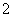
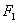 、
、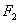 是一对相关曲线的焦点,
是一对相关曲线的焦点,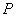 是它们在第一象限的交点,当
是它们在第一象限的交点,当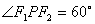 时,这一对相关曲线中双曲线的离心率是( )
时,这一对相关曲线中双曲线的离心率是( )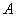 .
.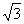
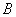 .
.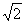
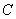 .
.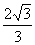
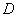 .
.
A
试题分析:设F1P=m,F2P=n,F1F2=2c,由余弦定理4c2=m2+n2-mn,设a1是椭圆的长半轴,a1是双曲线的实半轴,由椭圆及双曲线定义,得m+n=2a1,m-n=2a1,由此能求出结果.解:设F1P=m,F2P=n,F1F2=2c,由余弦定理得(2c)2=m2+n2-2mncos60°,即4c2=m2+n2-mn,设a1是椭圆的长半轴,a1是双曲线的实半轴,由椭圆及双曲线定义,得m+n=2a1,m-n=2a1,∴m=a1+a2,n=a1-a2,将它们及离心率互为倒数关系代入前式得a12-4a1a2+a12=0, a1=3a2,e1•e2=
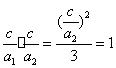 解得e2=
解得e2=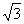 .故选A.
.故选A.点评:本题考查双曲线和椭圆的简单性质,解题时要认真审题,注意正确理解“相关曲线”的概念.

练习册系列答案
相关题目
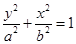 (
(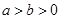 )离心率为
)离心率为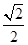 ,上顶点M,右顶点N,直线MN与圆
,上顶点M,右顶点N,直线MN与圆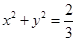 相切,斜率为k的直线l经过椭圆E在正半轴的焦点F,且交E于A、B不同两点.
相切,斜率为k的直线l经过椭圆E在正半轴的焦点F,且交E于A、B不同两点.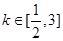 ,求m的取值范围.
,求m的取值范围.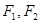 分别为双曲线
分别为双曲线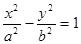 的左右焦点,点P在双曲线的右支上,且
的左右焦点,点P在双曲线的右支上,且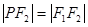 ,
,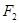 到直线
到直线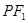 的距离等于双曲线的实轴长,则该双曲线的离心率为( )
的距离等于双曲线的实轴长,则该双曲线的离心率为( )
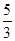
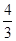
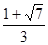
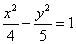 的中心和左焦点,点P为双曲线右支上的任意一点,则
的中心和左焦点,点P为双曲线右支上的任意一点,则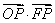 的最小值为( )
的最小值为( )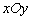 有相同的长度单位,以原点
有相同的长度单位,以原点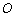 为极点,以
为极点,以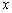 正半轴为极轴,已知曲线
正半轴为极轴,已知曲线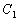 的极坐标方程为
的极坐标方程为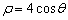 ,曲线
,曲线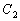 的参数方程是
的参数方程是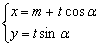 (
(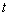 为参数,
为参数,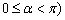 ,射线
,射线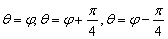 与曲线
与曲线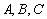
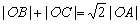 ;
;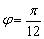 时,
时,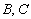 两点在曲线
两点在曲线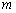 与
与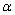 的值.
的值.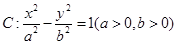 的离心率为
的离心率为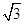 ,右准线方程为
,右准线方程为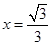 。
。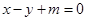 与双曲线C交于不同的两点A,B,且线段AB的中点在圆
与双曲线C交于不同的两点A,B,且线段AB的中点在圆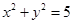 上,求实数m的值。
上,求实数m的值。 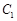 的极坐标方程是
的极坐标方程是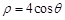 ,以极点为原点,极轴为
,以极点为原点,极轴为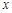 轴正方向建立平面直角坐标系,直线的参数方程是:
轴正方向建立平面直角坐标系,直线的参数方程是: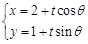 (为参数).
(为参数).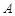 ,
,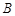 两点,点
两点,点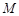 的直角坐标为
的直角坐标为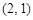 ,若
,若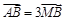 ,求直线的普通方程.
,求直线的普通方程.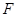 是抛物线
是抛物线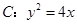 的焦点,
的焦点,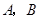 是
是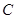 上的两个点,线段AB的中点为
上的两个点,线段AB的中点为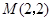 ,则
,则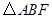 的面积等于
的面积等于 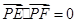 ,由点P向x轴作垂线段PQ,垂足为Q,点M满足
,由点P向x轴作垂线段PQ,垂足为Q,点M满足 ,点M的轨迹为C.
,点M的轨迹为C.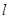 与曲线C交于A、B两点,点N满足
与曲线C交于A、B两点,点N满足