题目内容
已知曲线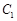 的极坐标方程是
的极坐标方程是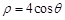 ,以极点为原点,极轴为
,以极点为原点,极轴为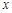 轴正方向建立平面直角坐标系,直线的参数方程是:
轴正方向建立平面直角坐标系,直线的参数方程是: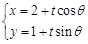 (为参数).
(为参数).
(Ⅰ)求曲线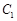 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线与曲线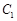 交于
交于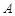 ,
,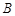 两点,点
两点,点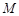 的直角坐标为
的直角坐标为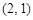 ,若
,若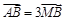 ,求直线的普通方程.
,求直线的普通方程.
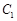 的极坐标方程是
的极坐标方程是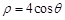 ,以极点为原点,极轴为
,以极点为原点,极轴为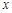 轴正方向建立平面直角坐标系,直线的参数方程是:
轴正方向建立平面直角坐标系,直线的参数方程是: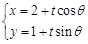 (为参数).
(为参数).(Ⅰ)求曲线
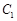 的直角坐标方程;
的直角坐标方程;(Ⅱ)设直线与曲线
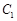 交于
交于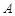 ,
,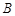 两点,点
两点,点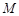 的直角坐标为
的直角坐标为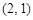 ,若
,若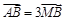 ,求直线的普通方程.
,求直线的普通方程.(Ⅰ)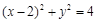 ;(Ⅱ)
;(Ⅱ)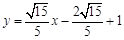 或
或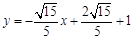 .
.
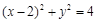 ;(Ⅱ)
;(Ⅱ)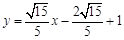 或
或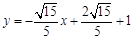 .
.试题分析:(Ⅰ)由
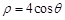 ,得
,得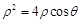 ,
,∵
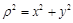 ,
,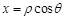
∴曲线
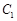 的直角坐标方程是
的直角坐标方程是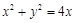 ,即
,即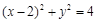 4分
4分(Ⅱ)设
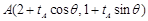 ,
,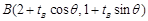
由已知
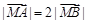 ,注意到
,注意到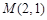 是直线参数方程恒过的定点,
是直线参数方程恒过的定点,∴
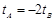 ①
①联立直线的参数方程与曲线
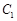 的直角坐标方程得:
的直角坐标方程得: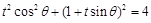 ,
,整理得:
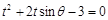 , 6分
, 6分∴
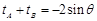 ,
,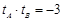 ,与①联立得:
,与①联立得: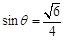 ,
,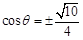
∴直线的参数方程为
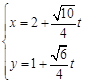 ,(为参数)或
,(为参数)或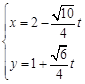 ,(为参数). 8分
,(为参数). 8分消去参数得的普通方程为
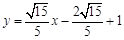 或
或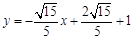 . 10分
. 10分点评:中档题,极坐标方程与直角坐标方程的互化,主要依据
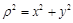 ,
,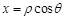 ,
,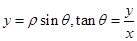 。应用直线的参数方程解题,往往要通过代入方程,得到关于参数的一元二次方程,应用韦达定理。
。应用直线的参数方程解题,往往要通过代入方程,得到关于参数的一元二次方程,应用韦达定理。
练习册系列答案
相关题目
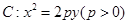 ,直线
,直线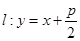 交抛物线于
交抛物线于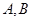 两点,且
两点,且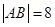 .
.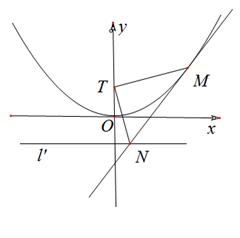
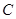 的方程;
的方程;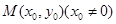 是抛物线
是抛物线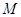 点的抛物线的切线与直线
点的抛物线的切线与直线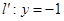 交于点
交于点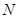 ,问在
,问在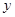 轴上是否存在定点
轴上是否存在定点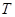 ,使得
,使得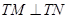 ?若存在,求出该定点,并求出
?若存在,求出该定点,并求出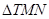 的面积的最小值;若不存在,请说明理由.
的面积的最小值;若不存在,请说明理由.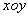 中,曲线
中,曲线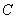 的参数方程为
的参数方程为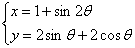 (
(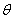 为参数)。
为参数)。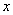 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线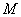 的极坐标方程为
的极坐标方程为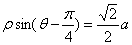 (其中
(其中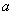 为常数)
为常数)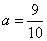 时,曲线
时,曲线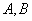 .求
.求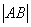 的值;
的值;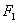 、
、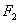 是一对相关曲线的焦点,
是一对相关曲线的焦点,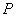 是它们在第一象限的交点,当
是它们在第一象限的交点,当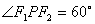 时,这一对相关曲线中双曲线的离心率是( )
时,这一对相关曲线中双曲线的离心率是( ) .
.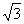
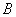 .
.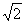
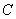 .
.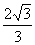
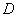 .
.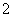
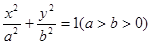 上一点,且
上一点,且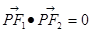 ,
,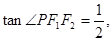 则该椭圆的离心率为( )
则该椭圆的离心率为( )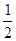
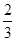
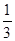
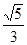
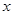 轴上的双曲线
轴上的双曲线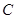 的离心率为
的离心率为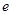 ,直线与双曲线
,直线与双曲线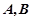 两点,线段
两点,线段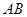 中点
中点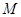 在第一象限,并且在抛物线
在第一象限,并且在抛物线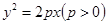 上,且
上,且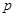 ,则直线的斜率为( )
,则直线的斜率为( )
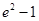
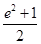
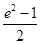
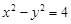 ,直线
,直线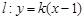 与该双曲线只有一个公共点,
与该双曲线只有一个公共点,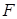 是抛物线
是抛物线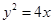 的焦点,准线与
的焦点,准线与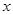 轴的交点为
轴的交点为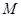 ,点
,点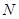 在抛物线上,且
在抛物线上,且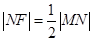 ,则
,则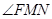 等于( )
等于( )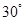
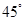

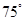
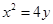 的焦点
的焦点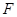 作倾斜角为
作倾斜角为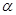 的直线交抛物线于
的直线交抛物线于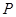 、
、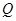 两点,过点
两点,过点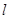 交
交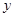 轴于点
轴于点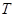 ,过点
,过点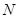 。
。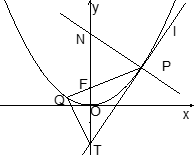
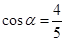 ,求此抛物线与线段
,求此抛物线与线段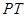 以及线段
以及线段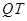 所围成的封闭图形的面积。
所围成的封闭图形的面积。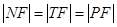 ;
;