题目内容
1.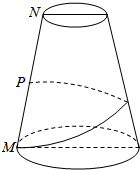 如图,已知圆台的上下底面半径分别为1cm和3cm,母线长为8cm,P是母线MN的中点,由M出发,沿圆台侧面绕一周到达点P,求经过的最短路程.
如图,已知圆台的上下底面半径分别为1cm和3cm,母线长为8cm,P是母线MN的中点,由M出发,沿圆台侧面绕一周到达点P,求经过的最短路程.
分析 由题意求出圆台所在圆锥的母线长,利用弧长公式求出圆心角,把最短路程转化为三角形的边长求解.
解答 解:沿母线MN剪开并展开如图,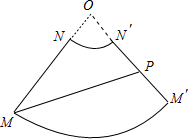
设ON=x,则由$\frac{x}{x+8}=\frac{1}{3}$,得x=4,
∴OM=12,
∵圆台底面半径为3,∴底面圆的周长为6π,则∠MOM′=$\frac{6π}{12}=\frac{π}{2}$.
在Rt△MOP中,由OM=12,OP=8,
∴MP=$\sqrt{1{2}^{2}+{8}^{2}}=4\sqrt{13}$.
∴经过的最短路程为$4\sqrt{13}$cm.
点评 本题考查旋转体表面上的最短距离问题,该类问题的解法是:首先剪展,然后在三角形中借助于正弦定理或余弦定理求解,是中档题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
12.下列四个推导过程符合演绎推理三段论形式且推理正确的是( )
| A. | 大前提:无限不循环小数是无理数;小前提:$\sqrt{11}$是无理数;结论:$\sqrt{11}$是无限不循环小数 | |
| B. | 大前提:无限不循环小数是无理数;小前提:$\sqrt{11}$是无限不循环小数;结论:$\sqrt{11}$是无理数 | |
| C. | 大前提:$\sqrt{11}$是无限不循环小数;小前提:无限不循环小数是无理数;结论:$\sqrt{11}$是无理数 | |
| D. | 大前提:$\sqrt{11}$是无限不循环小数;小前提:$\sqrt{11}$是无理数;结论:无限不循环小数是无理数 |
13.函数f(x)=$\frac{ax}{x-1}$满足f(f(x))=$\frac{4x}{x+1}$,则常数a=( )
| A. | 1 | B. | 2 | C. | -2或2 | D. | 1或2 |