题目内容
16.解方程:$\frac{8({x}^{2}+2x)}{{x}^{2}-1}$+$\frac{3({x}^{2}-1)}{{x}^{2}+2x}$=11.分析 利用换元法,化分式方程为整式方程,即可求解方程.
解答 解:设$\frac{{x}^{2}+2x}{{x}^{2}-1}$=t,则8t+$\frac{3}{t}$=11,
∴8t2-11t+3=0,
∴t=1或t=$\frac{3}{8}$.
t=1时,$\frac{{x}^{2}+2x}{{x}^{2}-1}$=1,∴x=-$\frac{1}{2}$;
t=$\frac{3}{8}$时,$\frac{{x}^{2}+2x}{{x}^{2}-1}$=$\frac{3}{8}$,∴x=-3或-$\frac{1}{5}$.
点评 本题考查解方程,考查学生分析解决问题的能力,比较基础.

练习册系列答案
相关题目
11.执行如图所示的程序框图,如果输出i=4,那么空白的判断框中应填入的条件是( )
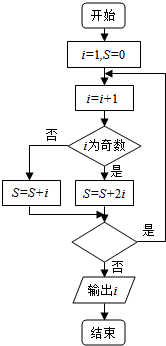

| A. | S≤10? | B. | S≤12? | C. | S≤14? | D. | S≤16? |
8.若某几何体的三视图如图所示,则这个几何体的直观图可以是( )
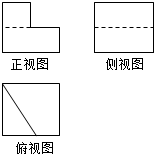

| A. | 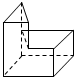 | B. | 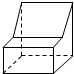 | C. |  | D. |  |
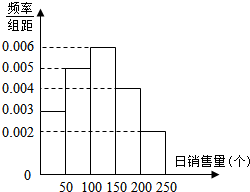 某校小卖部根据以往某种商品的销售记录,绘制了如下的日销售量频率分布直方图.若以日销售量的频率为概率,假设每天的销售量是相互独立的.结合直方图相关数据,以此来估计未来连续3天日销售量.
某校小卖部根据以往某种商品的销售记录,绘制了如下的日销售量频率分布直方图.若以日销售量的频率为概率,假设每天的销售量是相互独立的.结合直方图相关数据,以此来估计未来连续3天日销售量.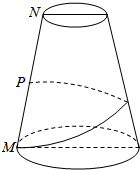 如图,已知圆台的上下底面半径分别为1cm和3cm,母线长为8cm,P是母线MN的中点,由M出发,沿圆台侧面绕一周到达点P,求经过的最短路程.
如图,已知圆台的上下底面半径分别为1cm和3cm,母线长为8cm,P是母线MN的中点,由M出发,沿圆台侧面绕一周到达点P,求经过的最短路程.