题目内容
已知函数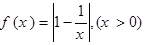
(1)当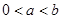 ,且
,且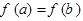 时,求证:
时,求证: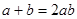
(2)是否存在实数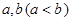 ,使得函数
,使得函数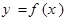 的定义域、值域都是
的定义域、值域都是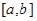 ?若存在,则求出
?若存在,则求出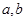 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
(1)证明见解析;(2)不存在,理由见解析.
解析试题分析:(1)分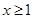 时和
时和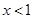 时,根据绝对值的性质,可根据绝对值的定义,可将函数的解析式化为分段函数的形式,进而分析函数的单调性,结合函数的单调性证得结论
时,根据绝对值的性质,可根据绝对值的定义,可将函数的解析式化为分段函数的形式,进而分析函数的单调性,结合函数的单调性证得结论
(2)根据(1)中结论,分①当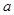 、
、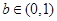 时,②当
时,②当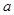 、
、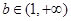 时,③当
时,③当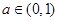 、
、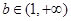 时,三种情况讨论
时,三种情况讨论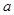 、
、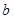 的存在性,最后综合讨论结果,可得答案.
的存在性,最后综合讨论结果,可得答案.
试题解析:(1)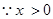 ,
,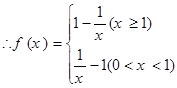 ,
,
所以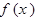 在(0,1)内递减,在(1,+
在(0,1)内递减,在(1,+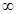 )内递增.
)内递增.
由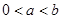 ,且
,且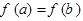
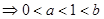 ,
,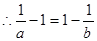 即
即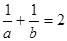 .
.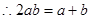
(2)不存在满足条件的实数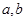 .
.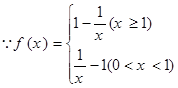
①当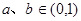 时,
时,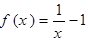 在(0,1)内递减,
在(0,1)内递减,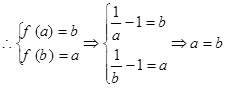 ,所以不存在.
,所以不存在.
②当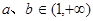 时,
时,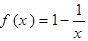 在(1,+
在(1,+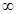 )内递增,
)内递增,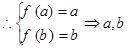 是方程
是方程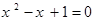 的根.
的根.
而方程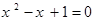 无实根.所以不存在.
无实根.所以不存在.
③当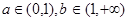 时,
时,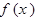 在(a,1)内递减,在(1,b)内递增,所以
在(a,1)内递减,在(1,b)内递增,所以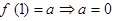 ,
,
由题意知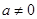 ,所以不存在.
,所以不存在.
考点:1.带绝对值的函数;2.分段函数.

练习册系列答案
相关题目
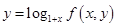 ,
, ,
,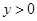 .
.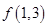 与
与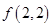 的大小;
的大小; ,证明:
,证明: ;
;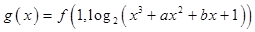 的图象为曲线
的图象为曲线 ,曲线
,曲线 处的切线斜率为
处的切线斜率为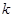 ,若
,若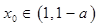 ,且存在实数
,且存在实数 ,使得
,使得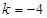 ,求实数
,求实数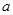 的取值范围.
的取值范围.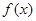 对任意实数
对任意实数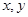 均有
均有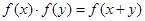 ,且当
,且当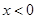 时
时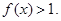
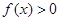 ;
;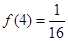 时, 对
时, 对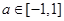 时恒有
时恒有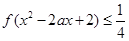 ,求实数
,求实数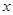 的取值范围.
的取值范围.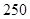 万元,每生产
万元,每生产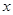 千件,需另投入成本为
千件,需另投入成本为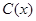 .当年产量不足
.当年产量不足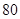 千件时,
千件时,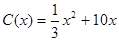 (万元).当年产量不小于
(万元).当年产量不小于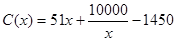 (万元).每件商品售价为
(万元).每件商品售价为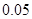 万元.通过市场分析,该厂生产的商品能全部售完.
万元.通过市场分析,该厂生产的商品能全部售完.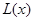 (万元)关于年产量
(万元)关于年产量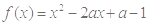 在区间[0,1]上有最小值-2,求
在区间[0,1]上有最小值-2,求 的值.
的值.
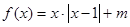
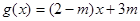 ,若方程
,若方程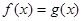 在
在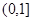 上有且仅一个实根,求实数
上有且仅一个实根,求实数 的取值范围;
的取值范围;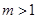 时,求函数
时,求函数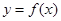 在
在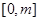 上的最大值.
上的最大值.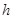 m,盖子边长为
m,盖子边长为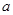 m,
m,
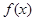 若存在
若存在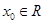 ,使得
,使得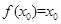 成立,则称
成立,则称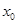 为
为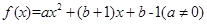
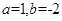 时,求函数
时,求函数 的不动点;
的不动点;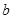 ,函数
,函数 的取值范围;
的取值范围;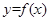 图象上
图象上 、
、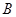 两点的横坐标是函数
两点的横坐标是函数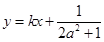 对称,求
对称,求 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为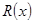 万元,且
万元,且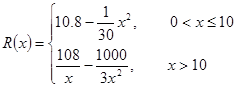 .
.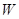 (万元)关于年产量
(万元)关于年产量