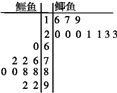
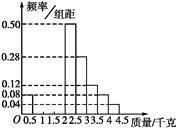
题目内容
【题目】已知全集U=R,集合A={x|1<2x<8},B={x| ![]() +1<0},C={x|a<x<a+1}.
+1<0},C={x|a<x<a+1}.
(1)求集合UA∩B;
(2)若B∪C=B,求实数a的取值范围.
【答案】
(1)解:∵全集U=R,集合A={x|1<2x<8}={x|0<x<3},
B={x| ![]() +1<0}={x|﹣2<x<4},
+1<0}={x|﹣2<x<4},
∴CUA={x|x≤0或x≥3},
∴UA∩B={x|﹣2<x≤0或3≤x<4}
(2)解:∵C={x|a<x<a+1},B∪C=B,
∴ ![]() ,解得﹣2<a<3.
,解得﹣2<a<3.
∴实数a的取值范围(﹣2,3)
【解析】(1)全集U=R,求出集合A,B,从而求出CUA,由此能求出UA∩B.(2)由C={x|a<x<a+1},B∪C=B,列出不等式组,能求出实数a的取值范围.
【考点精析】根据题目的已知条件,利用交、并、补集的混合运算的相关知识可以得到问题的答案,需要掌握求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案【题目】某学校课题组为了研究学生的数学成绩与学生细心程度的关系,在本校随机调查了100名学生进行研究.研究结果表明:在数学成绩及格的60名学生中有45人比较细心,另15人比较粗心;在数学成绩不及格的40名学生中有10人比较细心,另30人比较粗心.
(1)试根据上述数据完成2×2列联表;
数学成绩及格 | 数学成绩不及格 | 合计 | |
比较细心 | |||
比较粗心 | |||
合计 |
(2)能否在犯错误的概率不超过0.001的前提下认为学生的数学成绩与细心程度有关系. 参考数据:独立检验随机变量K2的临界值参考表:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() (其中n=a+b+c+d)
(其中n=a+b+c+d)