题目内容
【题目】已知曲线C1: ![]() ,(t为参数)曲线C2:
,(t为参数)曲线C2: ![]() +y2=4.
+y2=4.
(1)在同一平面直角坐标系中,将曲线C2上的点按坐标变换y′=yx,后得到曲线C′.求曲线C′的普通方程,并写出它的参数方程;
(2)若C1上的点P对应的参数为t= ![]() ,Q为C′上的动点,求PQ中点M到直线C3:
,Q为C′上的动点,求PQ中点M到直线C3: ![]() (t为参数)的距离的最小值.
(t为参数)的距离的最小值.
【答案】
(1)解:由 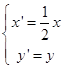 得到
得到 ![]() ①
①
将①代入曲线C2: ![]() +y2=4.得
+y2=4.得 ![]() +(y′)2=4,即(x′)2+(y′)2=4.
+(y′)2=4,即(x′)2+(y′)2=4.
因此椭圆 ![]() +y2=4经伸缩变换后得到的曲线方程是x2+y2=4.
+y2=4经伸缩变换后得到的曲线方程是x2+y2=4.
它的参数方程为 ![]()
(2)解:当t=π/2时,P(﹣4,4),Q(2cosθ,2sinθ),故M(﹣2+cosθ,2+sinθ)
曲线C3:为直线x﹣2y+8=0,
M到C3的距离d= ![]() |(﹣2+cosθ)﹣2(2+sinθ)+8|=
|(﹣2+cosθ)﹣2(2+sinθ)+8|= ![]() |cosθ﹣2sinθ+2|=
|cosθ﹣2sinθ+2|= ![]() |
| ![]() cos(θ+α)+2|
cos(θ+α)+2|
从而tanα=2时d的最小值为 ![]() |﹣
|﹣ ![]() +2|=
+2|= ![]()
【解析】(1)由 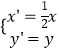 得到
得到 ![]() ,代入曲线C2:
,代入曲线C2: ![]() +y2=4.化简可得椭圆
+y2=4.化简可得椭圆 ![]() +y2=4经伸缩变换后得到的曲线方程.利用平方关系可得它的参数方程.(2)当t=
+y2=4经伸缩变换后得到的曲线方程.利用平方关系可得它的参数方程.(2)当t= ![]() 时,P(﹣4,4),Q(2cosθ,2sinθ),故M(﹣2+cosθ,2+sinθ).曲线C3:为直线x﹣2y+8=0,利用点到直线的距离公式可得M到C3的距离d=
时,P(﹣4,4),Q(2cosθ,2sinθ),故M(﹣2+cosθ,2+sinθ).曲线C3:为直线x﹣2y+8=0,利用点到直线的距离公式可得M到C3的距离d= ![]() |
| ![]() cos(θ+α)+2|,利用三角函数的单调性即可得出.
cos(θ+α)+2|,利用三角函数的单调性即可得出.

练习册系列答案
相关题目