Question

【题目】已知抛物线(为常数，)经过点，其对称轴在轴右侧，有下列结论:①抛物线经过点；②方程有两个不相等的实数根；③.其中，正确结论的个数为( )

A.0B.1C.2D.3

Answer 1

【答案】C

【解析】

① 由抛物线过点，对称轴在轴右侧，即可得出当时，结论①错误；

② 过点作轴的平行线，由该直线与抛物线有两个交点，可得出方程有两个不相等的实数根，结论②正确；

③ 由当时，可得出，由抛物线与轴交于点，可得出，进而即可得出，由抛物线过点可得出，结合，可得出，综上可得出，结论③正确，此题得解.

① 抛物线过点，对称轴在轴右侧，

当时，结论①错误；

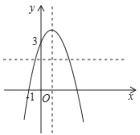
② 过点作轴的平行线，如图所示.

该直线与抛物线有两个交点，

方程有两个不相等的实数根，结论②正确；

③ 当时，

.

抛物线为常数且经过点，

，

.

当时，，即，

，

.

抛物线开口向下，

，

，

，结论③正确.

故选：