题目内容
【题目】已知双曲线E
的左、右焦点分别为F1，F2，P是双曲线E上的一点，且|PF2|＝2|PF1|，若直线PF2与双曲线E的渐近线交于点M，且M为PF2的中点，则双曲线E的渐近线方程为（ ）
A.y＝±
B.y＝±
C.y＝±2xD.y＝±3x
【答案】C
【解析】
画出图象，根据双曲线的定义及性质可得｜F1P｜＝2a，｜MF2｜＝2a，｜OM｜＝a，cos∠MOF2
，再根据余弦定理得齐次式，从而可求出渐近线方程．
解：画出图象如图：
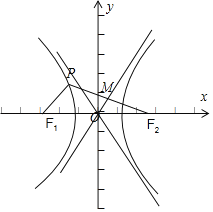
可得｜F1P｜＝2a，｜MF2｜＝2a，｜OM｜＝a，cos∠MOF2，
所以4a2＝a2+c2﹣2accos∠MOF1，
解得，5a2＝c2，即4a2＝b2，
所以
2，
所以双曲线的渐近线方程为：y＝±2x，
故选：C．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案【题目】据历年大学生就业统计资料显示：某大学理工学院学生的就业去向涉及公务员、教师、金融、公司和自主创业等五大行业2020届该学院有数学与应用数学、计算机科学与技术和金融工程等三个本科专业，毕业生人数分别是70人，140人和210人现采用.分层抽样的方法，从该学院毕业生中抽取18人调查学生的就业意向.
（1）应从该学院三个专业的毕业生中分别抽取多少人？
（2）国家鼓励大学生自主创业，在抽取的18人中，就业意向恰有三个行业的学生有5人为方便统计，将恰有三个行业就业意向的这5名学生分别记为
、
、
、
、
，统计如下表：
|
|
|
|
| |
公务员 | ○ | ○ | × | ○ | × |
教师 | ○ | × | ○ | × | ○ |
金融 | ○ | ○ | ○ | × | ○ |
公式 | × | × | ○ | ○ | ○ |
自主创业 | × | ○ | ○ | × |
其中“○”表示有该行业就业意向，“×”表示无该行业就业意向.
现从、、、、这5人中随机抽取2人接受采访.设
为事件“抽取的2人中至少有一人有自主创业意向”，求事件发生的概率.
【题目】2020年3月，国内新冠肺炎疫情得到有效控制，人们开始走出家门享受春光.某旅游景点为吸引游客，推出团体购票优惠方案如下表：
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
两个旅游团队计划游览该景点.若分别购票，则共需支付门票费1290元；若合并成个团队购票，则需支付门票费990元，那么这两个旅游团队的人数之差为（ ）
A.20B.25C.30D.40
