题目内容
【题目】设![]() 是正整数,集合
是正整数,集合![]() 是数集
是数集![]() 的一个子集,且
的一个子集,且![]() 中任意两个数的差不等于4或7.若
中任意两个数的差不等于4或7.若![]() 的元素个数的最大值记为
的元素个数的最大值记为![]() (如
(如![]() ,
,![]() ),试求
),试求![]() .
.
【答案】![]()
【解析】
易知1、4、6、7、9这五个数中的任意两个数的差都不是4或7,各加上11得到12、15、17、18、20,显然也是这样的数,且各与前五个数中的任意一个数的差也不是4或7.由此类推知,对于每个确定的正整数![]() ,每连续11个数中可取五个数,余下的
,每连续11个数中可取五个数,余下的![]() 个数中取
个数中取![]() 个数,一起组成集合
个数,一起组成集合![]() (
(![]() 表示不超过实数
表示不超过实数![]() 的最大整数).
的最大整数).
下面证明:![]() 中不可能包含更多的数.
中不可能包含更多的数.
倘若不然,则上述![]() 中前各11数组中至少有一组可以从中取六个数,使得任意两个数之差都不是4或7.
中前各11数组中至少有一组可以从中取六个数,使得任意两个数之差都不是4或7.
不妨考虑1,2,,11这组数,把它们分成五个小组:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中,至少要求有一组要取出两个数.显然,前四组中每组的两个数不能同取,最多一组取一个数,因此,只能在第五组
,其中,至少要求有一组要取出两个数.显然,前四组中每组的两个数不能同取,最多一组取一个数,因此,只能在第五组![]() 中取4、7.
中取4、7.
于是,![]() 中只能取1,
中只能取1,![]() 中只能取9,
中只能取9,![]() 中只能取6.
中只能取6.
这样,![]() 中3、10这两个数都不能取,从而知不可能取得第六个数.故
中3、10这两个数都不能取,从而知不可能取得第六个数.故
![]() .
.
当![]() 时,
时,![]() ;
;
当![]() 时,如
时,如![]() ,可考虑余下1,2,…,8这八个数,把它们分成四个组:
,可考虑余下1,2,…,8这八个数,把它们分成四个组:
![]() ,
,![]() ,
,![]() ,
,![]() ,每组取一个共4个,即
,每组取一个共4个,即![]() ;
;
当![]() 时,如
时,如![]() ,可考虑余下1,2,…,9这九个数,把它们分成五个组:
,可考虑余下1,2,…,9这九个数,把它们分成五个组:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,可取1、3、4、6、9这五个数,
,可取1、3、4、6、9这五个数,![]() .
.
因为![]() ,所以,
,所以,
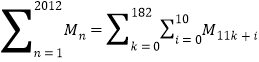
![]()
![]()
![]() .
.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】某中药种植基地有两处种植区的药材需在下周一、下周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘.由于下雨会影响药材品质,基地收益如下表所示:
周一 | 无雨 | 无雨 | 有雨 | 有雨 |
周二 | 无雨 | 有雨 | 无雨 | 有雨 |
收益 |
|
|
|
|
若基地额外聘请工人,可在周一当天完成全部采摘任务.无雨时收益为![]() 万元;有雨时,收益为
万元;有雨时,收益为![]() 万元.额外聘请工人的成本为
万元.额外聘请工人的成本为![]() 万元.
万元.
已知下周一和下周二有雨的概率相同,两天是否下雨互不影响,基地收益为![]() 万元的概率为
万元的概率为![]() .
.
(Ⅰ)若不额外聘请工人,写出基地收益![]() 的分布列及基地的预期收益;
的分布列及基地的预期收益;
(Ⅱ)该基地是否应该外聘工人,请说明理由.
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研.人社部从网上年龄在15-65岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
年龄 |
|
|
|
|
|
支持“延迟退休”的人数 | 15 | 5 | 15 | 28 | 17 |
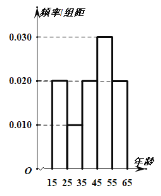
(1)由以上统计数据填2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
45岁以下 | 45岁以上 | 总计 | |
支持 | |||
不支持 | |||
总计 |
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() ,其中
,其中![]() .
.
(2)若以45岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动、现从这8人中随机抽2人.记抽到45岁以上的人数为X,求随机变量X的分布列及数学期望.
