Question

【题目】f(x)的定义域为(0，＋∞)，且对一切x>0，y>0都有f＝f(x)－f(y)，当x>1时，有f(x)>0。

(1)求f(1)的值；

(2)判断f(x)的单调性并证明；

(3)若f(6)＝1，解不等式f(x＋3)－f<2；

(4)若f(4)＝2，求f(x)在[1,16]上的值域。

Answer 1

【答案】(1)0,(2)见解析(3)(4)

【解析】

（1）利用赋值法令x=y，进行求解即可．

（2）利用抽象函数的关系，结合函数单调性的定义进行证明即可．

（3）利用函数单调性的性质将不等式进行转化求解即可．

（4）根据（2）的结论，将值域问题转化为求最值，根据f（4）=2，结合f（）=f（x）﹣f（y），赋值x=16，y=4，代入即可求得f（16），从而求得f（x）在[1，16]上的值域

（1）令x=y，f（1）=f（）=f（x）﹣f（x）=0，x＞0

（2）设0＜x1＜x2，则由f（）=f（x）﹣f（y），得f（x2）﹣f（x1）=f（），

∵＞1，∴f（）＞0．∴f（x2）﹣f（x1）＞0，即f（x）在（0，+∞）上是增函数

（3）∵f（6）=f（）=f（36）﹣f（6），∴f（36）=2，

原不等式化为f（x2+3x）＜f（36），∵f（x）在（0，+∞）上是增函数，

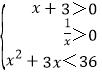∴解得0＜x＜．故原不等式的解集为（0，）

（4）由（2）知f（x）在[1，16]上是增函数．

∴f（x）min=f（1）=0，f（x）max=f（16）．

∵f（4）=2，由f（）=f（x）﹣f（y），知f（）=f（16）﹣f（4），

∴ f（16）=2f（4）=4，∴ f（x）在[1，16]上的值域为[0，4]