题目内容
【题目】若图所示,将若干个点摆成三角形图案,每条边(包括两个端点)n(n>1,n∈N*)个点,相应的图案中总的点数记为an , 则 ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() = .
= . 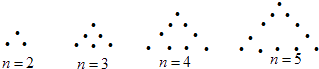
【答案】![]()
【解析】解:根据分析,可得
a2=3=3×(2﹣1),a3=6=3×(3﹣1),a4=9=3×(4﹣1),a5=12=3×(5﹣1)…an=3(n﹣1),
数列{an}是首项为3,公差为3的等差数列,通项为an=3(n﹣1)(n≥2);
所以 ![]() =
= ![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() ),
),
则 ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() =1﹣
=1﹣ ![]() +
+ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】利用归纳推理对题目进行判断即可得到答案,需要熟知根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理.

练习册系列答案
相关题目