题目内容
 是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国
是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国 标准采用世卫组织设定的最宽限值,
标准采用世卫组织设定的最宽限值, 日均值在35微克/立方米以下空气质量为一级;在35微克/立方米
日均值在35微克/立方米以下空气质量为一级;在35微克/立方米 75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.
75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.
某试点城市环保局从该市市区2011年全年每天的 监测数据中随机抽取6天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶),若从这6天的数据中随机抽出2天.
监测数据中随机抽取6天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶),若从这6天的数据中随机抽出2天.
(Ⅰ)求恰有一天空气质量超标的概率;
(Ⅱ)求至多有一天空气质量超标的概率.
(Ⅰ)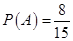 ;(Ⅱ)
;(Ⅱ)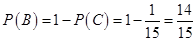 .
.
解析试题分析:由茎叶图知:6天有4天空气质量未超标,有2天空气质量超标. …………2分
记未超标的4天为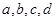 ,超标的两天为
,超标的两天为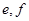 .则从6天中抽取2天的所有情况为:
.则从6天中抽取2天的所有情况为: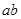 ,
, ,
,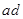 ,
,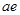 ,
, ,
,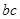 ,
, ,
,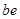 ,
,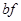 ,
,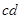 ,
, ,
,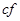 ,
,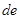 ,
,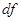 ,
,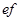 ,基本事件数为15.…………4分
,基本事件数为15.…………4分
(Ⅰ)记 “6天中抽取2天,恰有1天空气质量超标”为事件 ,可能结果为:
,可能结果为: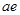 ,
, ,
,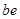 ,
,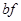 ,
, ,
,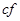 ,
,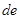 ,
,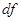 ,基本事件数为
,基本事件数为 .
.
∴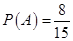 ;……………6分
;……………6分
(Ⅱ)记“至多有一天空气质量超标”为事件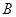 ,
,
“2天都超标”为事件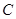 ,其可能结果为
,其可能结果为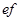 ,…………………………8分
,…………………………8分
故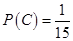 ,…………………………………………………………10分
,…………………………………………………………10分
∴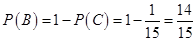 . …………………………………12分
. …………………………………12分
考点:本题主要考查茎叶图,古典概型概率的计算。
点评:中档题,统计中的抽样方法,频率直方图,概率计算及分布列问题,是高考必考内容及题型。古典概型概率的计算问题,关键是明确基本事件数,往往借助于“树图法”,做到不重不漏。(II)中利用了相互对立事件的概率公式,简化了计算过程。

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案某校为了解高二学生 、
、 两个学科学习成绩的合格情况是否有关, 随机抽取了该年级一次期末考试
两个学科学习成绩的合格情况是否有关, 随机抽取了该年级一次期末考试 、
、 两个学科的合格人数与不合格人数,得到以下2
两个学科的合格人数与不合格人数,得到以下2 2列联表:
2列联表:
| |  学科合格人数 学科合格人数 |  学科不合格人数 学科不合格人数 | 合计 |
 学科合格人数 学科合格人数 | 40 | 20 | 60 |
 学科不合格人数 学科不合格人数 | 20 | 30 | 50 |
| 合计 | 60 | 50 | 110 |
 学科合格”与“
学科合格”与“ 学科合格”有关;
学科合格”有关;(2)从“
 学科合格”的学生中任意抽取2人,记被抽取的2名学生中“
学科合格”的学生中任意抽取2人,记被抽取的2名学生中“ 学科合格”的人数为
学科合格”的人数为 ,求
,求 的数学期望.
的数学期望.附公式与表:

 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下.记成绩不低于90分者为“成绩优秀”.
(1)在乙班样本的20个个体中,从不低于86分的成绩中随机抽取2个,求抽出的2个至多一个“成绩优秀”的概率;
(2)由以上统计数据填写下面列联表,并判断是否有90%的把握认为:“成绩优秀”与教学方式有关.
| | 甲班 (A方式) | 乙班 (B方式) | 总计 |
| 成绩优秀 | | | |
| 成绩不优秀 | | | |
| 总计 | | | |

 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2. 706 | 3. 841 | 5. 024 |
某校为了解学生的学科学习兴趣,对初高中学生做了一个喜欢数学和喜欢语文的抽样调查,随机抽取了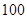 名学生,相关的数据如下表所示:
名学生,相关的数据如下表所示:
| | 数学 | 语文 | 总计 |
| 初中 | 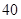 | 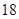 | 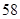 |
| 高中 | 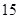 | 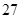 | 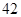 |
| 总计 | 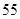 | 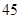 | 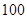 |
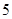 名,高中学生应该抽取几名?
名,高中学生应该抽取几名?(2) 在(1)中抽取的
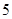 名学生中任取
名学生中任取 名,求恰有
名,求恰有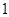 名初中学生的概率.
名初中学生的概率.  内.现根据所得数据画出了该样本的频率分布直方图如下.(每个分组包括左端点,不包括右端点,如第一组表示月收入在
内.现根据所得数据画出了该样本的频率分布直方图如下.(每个分组包括左端点,不包括右端点,如第一组表示月收入在 内)
内)
 内的频率;
内的频率; 内的居民中抽取多少人?
内的居民中抽取多少人?
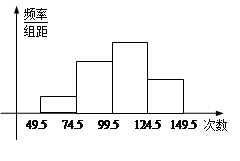
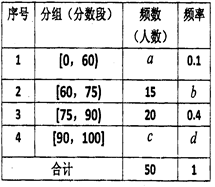
 的值;
的值;