题目内容
14.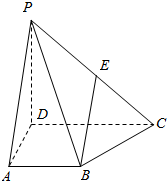 四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,AD⊥DC,侧棱PD⊥底面ABCD,且AB=AD=1,PD=DC=2,E是PC的中点.
四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,AD⊥DC,侧棱PD⊥底面ABCD,且AB=AD=1,PD=DC=2,E是PC的中点.(Ⅰ)求证:BE∥平面PAD;
(Ⅱ)线段PB上是否存在一点Q,使得PC⊥平面ADQ?若存在,求出$\frac{PB}{QB}$的值;若不存在,请说明理由.
分析 (I)以D为坐标原点,以DA、DC、DP所在直线依次为x轴、y轴、z轴建立空间直角坐标系,由向量法得到AF∥BE,由此能证明BE∥平面PAD.
(II)假设线段PB上存在一点Q,使PC⊥平面ADQ,设$\frac{PB}{QB}=λ(λ>0)$,由向量法能求出λ=3,由此得到线段PB上存在一点Q,使得PC⊥平面ADQ,且$\frac{PB}{QB}=3$.
解答 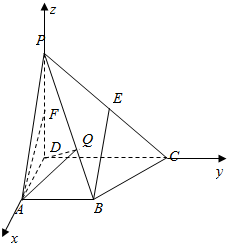 (I)证明:以D为坐标原点,以DA、DC、DP所在直线依次为x轴、y轴、z轴建立空间直角坐标系,…1分
(I)证明:以D为坐标原点,以DA、DC、DP所在直线依次为x轴、y轴、z轴建立空间直角坐标系,…1分
则D(0,0,0),A(1,0,0),B(1,1,0),C(0,2,0),P(0,0,2),E(0,1,1)…2分
取PD中点F,连结AF,F(0,0,1),$\overrightarrow{AF}=(-1,0,1)$,…3分
$\overrightarrow{BE}=(-1,0,1)$,∴$\overrightarrow{AF}$=$\overrightarrow{BE}$…4分
即AF∥BE…5分
而AF?平面PDA,且BE?平面PDA
∴BE∥平面PAD…6分
(II)解:假设线段PB上存在一点Q,使PC⊥平面ADQ,设$\frac{PB}{QB}=λ(λ>0)$
设Q(x,y,z),则$\overrightarrow{PB}=λ\overrightarrow{QB}$,即(1,1,-2)=λ(1-x,1-y,-z)…8分
∴$x=1-\frac{1}{λ},y=1-\frac{1}{λ},z=\frac{2}{λ}$…9分
$\overrightarrow{DA}=({1,0,0}),\overrightarrow{DQ}=({x,y,z}),\overrightarrow{PC}=({0,2,-2})$
∵PC⊥平面ADQ,∴$\left\{{\begin{array}{l}{\overrightarrow{PC•}\overrightarrow{DA}=0}\\{\overrightarrow{PC}•\overrightarrow{DQ}=2y-2z=0}\end{array}}\right.$,∴y=z,…10分
即$1-\frac{1}{λ}=\frac{2}{λ}$,∴λ=3
∴线段PB上存在一点Q,使得PC⊥平面ADQ,且$\frac{PB}{QB}=3$.…13分.
点评 本题考查线面平行的证明,考查使得线面垂直的点是否存在的判断与求法,是中档题,解题时要认真审题,注意向量法的合理运用.

| A. | ($\frac{2}{3}$,1) | B. | (0,1) | C. | (0,$\frac{2}{3}$) | D. | (0,$\frac{2}{3}$] |
| A. | 2 | B. | 5 | C. | 1 | D. | -1 |
| A. | 开口向上 | B. | 开口向下 | C. | 开口向左 | D. | 开口向右 |
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
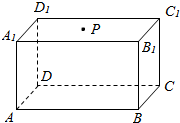 如图,P为长方体ABCD-A1B1C1D1的上底面A1B1C1D1内的一点,过直线BC与点P的平面记为α,若α∩平面A1B1C1D1=l
如图,P为长方体ABCD-A1B1C1D1的上底面A1B1C1D1内的一点,过直线BC与点P的平面记为α,若α∩平面A1B1C1D1=l