题目内容

17．已知0＜a＜1，若loga$\frac{2}{3}$＜1，则实数a的取值范围是（　　）
A．（$\frac{2}{3}$，1）B．（0，1）C．（0，$\frac{2}{3}$）D．（0，$\frac{2}{3}$]

分析 直接利用指数函数的单调性，化简求解不等式的解集．

解答 解：0＜a＜1，loga$\frac{2}{3}$＜1=logaa，
可得$\frac{2}{3}＜a＜1$．
故选：A．

点评 本题考查指数不等式的解法，考查计算能力．

练习册系列答案
相关题目
7．已知|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=2．
（1）若$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°，求|2$\overrightarrow{a}$-$\overrightarrow{b}$|；
（2）若向量k$\overrightarrow{a}$+$\overrightarrow{b}$与k$\overrightarrow{a}$-$\overrightarrow{b}$互相垂直，求k的值．
8．下列函数中，与函数y=-x的奇偶性，单调性都相同的是（　　）
A．y=$\frac{1}{x}$B．y=-sinxC．y=-lnxD．y=lg（$\sqrt{{x}^{2}+1}$-x）
5．在某次测量中得到的A样本数据如下；74，74，79，79，86，87，87，90，91，92．若B样本数据恰好是A样本数据每个都加5后所得数据，则A，B两样本的下列数字特征对应相同的是（　　）
A．众数B．平均数C．中位数D．标准差
12．已知函数f（x）=lg（ax-1）（a＞0，且a≠1），求f（x）的定义域．
2．函数y=$\frac{cosx}{\sqrt{1-si{n}^{2}x}}$+$\frac{\sqrt{1-co{s}^{2}x}}{sinx}$的值域为{2，0，-2}．
9．在复平面内，复数3-4i，2-6i对应向量分别为$\overrightarrow{OA}，\overrightarrow{OB}$．其中O是坐标原点，向量$\overrightarrow{BA}$对应复数z，则|z|的值为（　　）
A．5B．$\sqrt{5}$C．$\sqrt{101}$D．$\sqrt{29}$
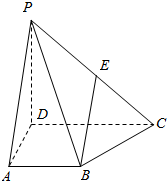14．四棱锥P-ABCD中，底面ABCD是直角梯形，AB∥DC，AD⊥DC，侧棱PD⊥底面ABCD，且AB=AD=1，PD=DC=2，E是PC的中点．
（Ⅰ）求证：BE∥平面PAD；
（Ⅱ）线段PB上是否存在一点Q，使得PC⊥平面ADQ？若存在，求出$\frac{PB}{QB}$的值；若不存在，请说明理由．
15．函数f（x）=ax2+bx+c的图象如图所示，M=|a-b+c|+|2a+b|，N=|a+b+c|+|2a-b|则（　　）
A．M＞N?B．M=N?
C．M＜N?D．M、N 的大小关系不确定

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网