题目内容
2．已知数列{an}满足a1=1，an+1=2an（n∈N*），则an=2n-1．分析 利用等比数列的通项公式即可得出．
解答 解：∵数列{an}满足a1=1，an+1=2an（n∈N*），
∴数列{an}是等比数列，首项为1，公比为2．
∴${a}_{n}={2}^{n-1}$．
故答案为：2n-1．
点评 本题考查了等比数列的通项公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
轻松暑假总复习系列答案
相关题目
12．已知直线y=m（0＜m＜2）与函数y=sinωx+$\sqrt{3}$cosωx（ω＞0）的图象依次交于A（1，m），B（5，m），C（7，m）三点，则ω=（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{2}$ | D． | $\frac{π}{6}$ |
13．若一个四棱锥的底面是边长为4的正方形，各侧棱都等于3，那么这个四棱锥的高等于（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | 5 | D． | $\sqrt{7}$ |
7．已知全集U=R，集合A={x|0＜log2x＜2}，B={y|y=x2+2}，则（CUB）∩A=（ ）
| A． | （1，2） | B． | （1，4） | C． | [2，4） | D． | （0，2） |
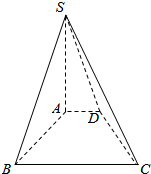已知四棱锥S-ABCD中，底面ABCD是直角梯形，∠ABC=90°，AD∥BC，SA=AB=BC=2，AD=1，SA⊥底面ABCD．