Question

【题目】设正项数列的前项和，且满足.

（Ⅰ）计算的值，猜想的通项公式，并证明你的结论；

（Ⅱ）设是数列的前项和，证明：.

Answer 1

【答案】(1) （2）见解析

【解析】试题分析：（1）先根据 关系，将条件转化为项与项递推关系，依次代入求解，可得的值，根据规律猜想，利用项与项递推关系及归纳假设证明n=k+1时情况（2）利用放缩裂项求和：，也可直接利用数学不等式进行证明

试题解析：（Ⅰ）解：当n=1时，，得；，得；

，得.

猜想

证明：（ⅰ）当n=1时，显然成立.

（ⅱ）假设当n=k时，

则当n=k+1时，

结合，解得

于是对于一切的自然数，都有

（Ⅱ）证法一：因为，

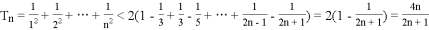
证法二：数学归纳法

证明：（ⅰ）当n=1时，，，

（ⅱ）假设当n=k时，

则当n=k+1时，

要证：只需证：

由于

所以

于是对于一切的自然数，都有