题目内容
9.在平面直角坐标系xOy中,已知直线l的方程为2x+(k-3)y-2k+6=0,k∈R.(1)若直线l在x轴,y轴上的截距之和为1,求坐标原点O到直线l的距离;
(2)求坐标原点O到直线l距离的最大值;
(3)若直线l与直线l1:2x-y-2=0和l2:x+y+3=0分别相交于A,B两点,点P(0,2)到A,B两点的距离相等,求k的值.
分析 直线l的方程为2x+(k-3)y-2k+6=0,k∈R.化为(2x-3y+6)+k(y-2)=0.
联立$\left\{\begin{array}{l}{2x-3y+6=0}\\{y-2=0}\end{array}\right.$,解得定点P(0,2).
(1)设直线l的方程为:$\frac{x}{a}+\frac{y}{b}$=1,则$\left\{\begin{array}{l}{\frac{2}{b}=1}\\{a+b=1}\end{array}\right.$,解得a,b,可得直线l的方程,再利用点到直线的距离公式公式即可得出;
(2)由于直线l的方程2x+(k-3)y-2k+6=0,k∈R,经过定点P(0,2).即可得出坐标原点O到直线l距离的最大值.
(3)设A(s,t),由于点P在已知直线l上,且点P(0,2)到A,B两点的距离相等,利用中点坐标公式可得B(-s,4-t).联立$\left\{\begin{array}{l}{2s-t-2=0}\\{-s+4-t+3=0}\end{array}\right.$,解得即可得出.
解答 解:直线l的方程为2x+(k-3)y-2k+6=0,k∈R.化为(2x-3y+6)+k(y-2)=0.
联立$\left\{\begin{array}{l}{2x-3y+6=0}\\{y-2=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$,即过定点P(0,2).
(1)设直线l的方程为:$\frac{x}{a}+\frac{y}{b}$=1,则$\left\{\begin{array}{l}{\frac{2}{b}=1}\\{a+b=1}\end{array}\right.$,解得b=2,a=-1.
∴直线l的方程为:$\frac{x}{-1}+\frac{y}{2}$=1,化为2x-y+2=0.
∴坐标原点O到直线l的距离d=$\frac{|0+2|}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$.
(2)由于直线l的方程2x+(k-3)y-2k+6=0,k∈R,经过定点P(0,2).
∴坐标原点O到直线l距离的最大值为2.
(3)设A(s,t),∵点P在已知直线l上,且点P(0,2)到A,B两点的距离相等,
∴B(-s,4-t).
∴$\left\{\begin{array}{l}{2s-t-2=0}\\{-s+4-t+3=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{s=3}\\{t=4}\end{array}\right.$,∴A(3,4).
代入直线l的方程2x+(k-3)y-2k+6=0,可得2×3+4(k-3)-2k+6=0,
解得k=0.
点评 本题考查了直线的交点坐标、直线过定点问题、点到直线的距离公式、中点坐标公式,考查了推理能力与计算能力,属于中档题.

 小学期末标准试卷系列答案
小学期末标准试卷系列答案| A. | 3y<3x | B. | x3>y3 | C. | log4x<log4y | D. | ($\frac{1}{4}$)x<($\frac{1}{4}$)y |
| 水深x(m) | 1.6 | 1.7 | 1.8 | 1.9 | 2.0 |
| 流速y(m/s) | 1 | 1.5 | 2 | 2.5 | 3 |
(2)若y与x之间具有线性相关关系,求y对x的回归直线方程; ($\sum_{i=1}^5{x_i^2}=16.3$,$\sum_{i=1}^5{{x_i}{y_i}}=18.5$)
(3)预测水深为1.95m水的流速是多少.
参考公式:$b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}}$$a=\overline y-b\overline x$.
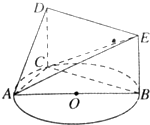 如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=$\frac{1}{2}$.
如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=$\frac{1}{2}$.