题目内容
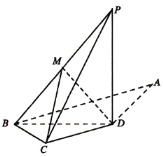
【题目】已知正四棱锥![]() 的底面边长为
的底面边长为![]() 高为
高为![]() 其内切球与面
其内切球与面![]() 切于点
切于点![]() ,球面上与
,球面上与![]() 距离最近的点记为
距离最近的点记为![]() ,若平面
,若平面![]() 过点
过点![]() ,
,![]() 且与
且与![]() 平行,则平面
平行,则平面![]() 截该正四棱锥所得截面的面积为______.
截该正四棱锥所得截面的面积为______.
【答案】![]()
【解析】
取![]() 中点
中点![]() ,连
,连![]() ,取
,取![]() 中点
中点![]() ,连
,连![]() ,则
,则![]() 平面
平面![]() ,根据已知可得
,根据已知可得![]() 为正三角形,正棱锥
为正三角形,正棱锥![]() 内切球的球心为正
内切球的球心为正![]() 的内心
的内心![]() ,与面
,与面![]() 切于点
切于点![]() 为
为![]() 中点,球面上与
中点,球面上与![]() 距离最近的点为
距离最近的点为![]() 与球面的交点,即在
与球面的交点,即在![]() 之间且
之间且![]() 长为内切球的半径,连
长为内切球的半径,连![]() 并延长交
并延长交![]() 于
于![]() ,平面
,平面![]() 过
过![]() 与
与![]() 平行,可得平面
平行,可得平面![]() 分别与平面
分别与平面![]() 、平面
、平面![]() 的交线为过
的交线为过![]() 与
与![]() 平行的直线,即可得到截面为梯形,根据长度关系,即可求解.
平行的直线,即可得到截面为梯形,根据长度关系,即可求解.
取![]() 中点
中点![]() ,连
,连![]() ,取
,取![]() 中点
中点![]() ,连
,连![]() ,
,
则![]() ,
,![]() 为正方形
为正方形![]() 的中心,四棱锥
的中心,四棱锥![]() 是正四棱锥,
是正四棱锥,
所以![]() 平面
平面![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
同理![]() ,所以
,所以![]() 为正三角形,
为正三角形,
所以正四棱锥![]() 内切球的球心为正
内切球的球心为正![]() 的内心
的内心![]() ,
,
内切球的半径是正![]() 的内切圆半径为
的内切圆半径为![]() ,
,
内切球与平面![]() 的切点
的切点![]() 为正
为正![]() 内切圆与直线
内切圆与直线![]() 的切点,
的切点,
所以![]() 为
为![]() 中点,球面上与
中点,球面上与![]() 距离最近的点为连
距离最近的点为连![]() 与球面的交点,
与球面的交点,
即在![]() 之间,且
之间,且![]() ,因此
,因此![]() 为
为![]() 中点,
中点,
连![]() 并延长交
并延长交![]() 于
于![]() ,平面
,平面![]() 过
过![]() 与直线
与直线![]() 平行,
平行,
设平面![]() 分别与平面
分别与平面![]() 、平面
、平面![]() 交于
交于![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() ,又因为
,又因为![]() ,
,![]() ,
,
所以![]() ,同理可证
,同理可证![]() ,所以
,所以![]() ,连
,连![]() ,
,
则梯形![]() 为所求的截面,因为
为所求的截面,因为![]() ,
,
![]() ,所以
,所以![]() 平面
平面![]() 平面
平面![]() ,
,
所以![]() ,所以
,所以![]() ,
,
连![]() ,则
,则![]() 为
为![]() 的角平分线,所以
的角平分线,所以![]() ,
,
又因为![]() 分别为
分别为![]() 的中点,所以
的中点,所以![]() ,
,
所以![]() ,而
,而![]() ,所以
,所以![]() ,
,
所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
所以截面梯形![]() 的面积
的面积![]() .
.
故答案为:![]() .
.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目