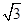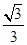题目内容
已知椭圆中心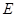 在坐标原点,焦点在
在坐标原点,焦点在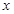 轴上,且经过
轴上,且经过 、
、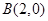 、
、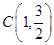 三点.
三点.
(1)求椭圆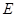 的方程;
的方程;
(2)设直线 与椭圆
与椭圆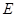 交于
交于 、
、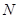 两点.
两点.
①若 ,求
,求 的长;
的长;
②证明:直线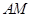 与直线
与直线 的交点在直线
的交点在直线 上.
上.
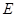 在坐标原点,焦点在
在坐标原点,焦点在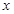 轴上,且经过
轴上,且经过 、
、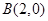 、
、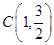 三点.
三点.(1)求椭圆
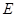 的方程;
的方程;(2)设直线
 与椭圆
与椭圆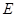 交于
交于 、
、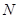 两点.
两点.①若
 ,求
,求 的长;
的长;②证明:直线
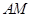 与直线
与直线 的交点在直线
的交点在直线 上.
上.解:(1)设椭圆方程为 ……1分
……1分
将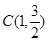 代入椭圆E的方程,得
代入椭圆E的方程,得
 ,解得
,解得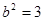 ∴椭圆
∴椭圆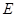 的方程
的方程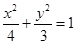 ……3分
……3分
(2)

……5分
①若 ,则
,则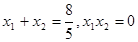
又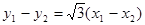 ……6分
……6分
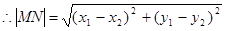 =
=
=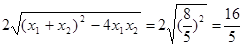 ……8分
……8分
②

因此结论成立.直线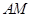 与直线
与直线 的交点住直线
的交点住直线 上. ……14分
上. ……14分
 ……1分
……1分 将
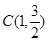 代入椭圆E的方程,得
代入椭圆E的方程,得 ,解得
,解得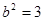 ∴椭圆
∴椭圆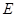 的方程
的方程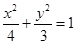 ……3分
……3分(2)

……5分
①若
 ,则
,则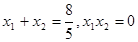
又
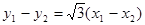 ……6分
……6分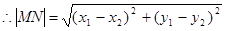 =
=
=
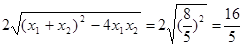 ……8分
……8分②

因此结论成立.直线
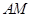 与直线
与直线 的交点住直线
的交点住直线 上. ……14分
上. ……14分略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的离心率为
的离心率为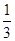 ,椭圆上的点到右焦点F的最近距离为2,若椭圆C与x轴交于A、B两点,M是椭圆C上异于A、B的任意一点,直线MA交直线
,椭圆上的点到右焦点F的最近距离为2,若椭圆C与x轴交于A、B两点,M是椭圆C上异于A、B的任意一点,直线MA交直线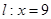 于G点,直线MB交直线
于G点,直线MB交直线 于H点。
于H点。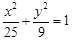 ,F是右焦点,
,F是右焦点,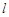 是过点F的一条直线(不与
是过点F的一条直线(不与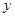 轴平行),交椭圆于A、B两点,
轴平行),交椭圆于A、B两点, 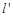 是AB的中垂线,交椭圆的长轴于一点D,则
是AB的中垂线,交椭圆的长轴于一点D,则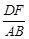 的值是 .
的值是 .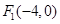 ,
,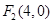 ,P在椭圆上,若 △
,P在椭圆上,若 △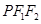 的面积的最大值为12,则椭圆方程为
的面积的最大值为12,则椭圆方程为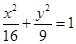
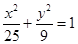
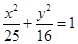
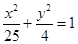
 的左、右焦点分别为F1、F2,A是椭圆C上的一点,
的左、右焦点分别为F1、F2,A是椭圆C上的一点,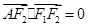 ,坐标原点O到直线AF1的距离为
,坐标原点O到直线AF1的距离为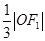 .
. ,交 y轴于点M,若
,交 y轴于点M,若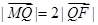 ,求直线l 的斜率.
,求直线l 的斜率.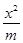 + y2=1(m>1)和双曲线
+ y2=1(m>1)和双曲线 - y2=1(n>0),P是它们的一个交点,则ΔF1PF2的形状是( )
- y2=1(n>0),P是它们的一个交点,则ΔF1PF2的形状是( )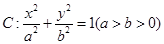 恒过定点
恒过定点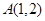 ,则椭圆的中心到准线的距离的
,则椭圆的中心到准线的距离的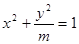 的下焦点为
的下焦点为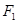 、上焦点为
、上焦点为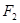 ,其离心 率
,其离心 率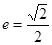 。过焦点F2且与
。过焦点F2且与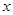 轴不垂直的直线l交椭圆于A、B两点。
轴不垂直的直线l交椭圆于A、B两点。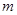 的值;
的值;  上的点,F1、F2分别是椭圆的左、右焦点,若
上的点,F1、F2分别是椭圆的左、右焦点,若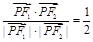 ,则
,则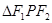 的面积为( )
的面积为( )