题目内容
如果f(x)为偶函数,且f(x)导数存在,则f′(0)的值为( )
| A.2 | B.1 | C.0 | D.﹣1 |
C
因为f(x)为偶函数,所以f(x)=f(﹣x),
此时两边对x求导得:f′(x)=﹣f′(﹣x),
又因为f′(0)存在,
把x=0代入得:f′(0)=﹣f′(0),
解得f′(0)=0.
故选C
此时两边对x求导得:f′(x)=﹣f′(﹣x),
又因为f′(0)存在,
把x=0代入得:f′(0)=﹣f′(0),
解得f′(0)=0.
故选C

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
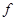 (
(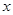 ) =
) =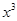 ,g (
,g (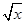 。
。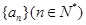 满足
满足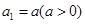 ,
,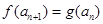 ,证明:存在常数M,使得对于任意的
,证明:存在常数M,使得对于任意的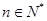 ,都有
,都有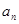 ≤
≤ 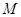 .
. ,
, .
. ,使得
,使得 ,求a的取值范围;
,求a的取值范围; 有两个不同的实数解
有两个不同的实数解 ,证明:
,证明: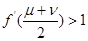 .
.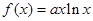 ,
,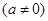 .
.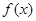 的单调区间;
的单调区间;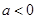 时,若对于任意的
时,若对于任意的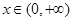 ,都有
,都有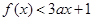 成立,求
成立,求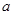 的取值范围.
的取值范围.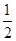 x2(a>0),若对任意两个不等的正实数x1,x2都有
x2(a>0),若对任意两个不等的正实数x1,x2都有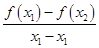 >2恒成立,则a的取值范围是________.
>2恒成立,则a的取值范围是________.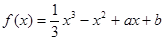 ,
,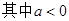 ,如果存在实数
,如果存在实数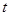 ,使
,使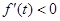 ,则
,则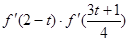 的值( )
的值( )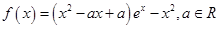 .
.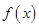 在
在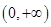 内单调递增,求
内单调递增,求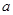 的取值范围;
的取值范围;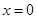 处取得极小值,求
处取得极小值,求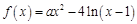 ,
,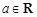 .
.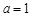 时,求
时,求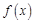 的单调区间;
的单调区间;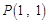 和函数
和函数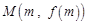 ,对任意
,对任意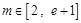 ,直线
,直线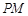 倾斜角都是钝角,求
倾斜角都是钝角,求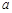 的取值范围.
的取值范围.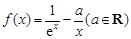 .若存在实数
.若存在实数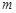 ,
,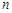 ,使得
,使得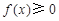 的解集恰为
的解集恰为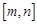 ,则
,则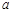 的取值范围是 .
的取值范围是 .