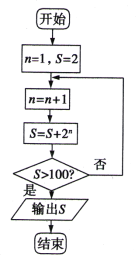
题目内容
【题目】如图:在四棱锥![]() 中,
中,![]() 平面
平面![]() .
.![]() ,
,![]() ,
,![]() .点
.点![]() 是
是![]() 与
与![]() 的交点,点
的交点,点![]() 在线段
在线段![]() 上且
上且![]() .
.
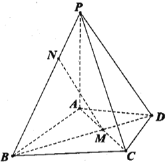
(1)证明:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)求二面角![]() 的正切值.
的正切值.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)推导出![]() ,在正三角形
,在正三角形![]() 中,
中,![]() ,从而
,从而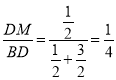 .
.
进而![]() ,由此能证明
,由此能证明![]() 平面
平面![]() ;
;
(2)分别以![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图的空间直角坐标系,求出
轴建立如图的空间直角坐标系,求出![]() 与平面
与平面![]() 的法向量
的法向量![]() ,进而利用向量的夹角公式可求出直线
,进而利用向量的夹角公式可求出直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)求出面![]() 与面
与面![]() 的法向量,进而利用向量的夹角公式可求出二面角
的法向量,进而利用向量的夹角公式可求出二面角![]() 的平面角的余弦值,再转化为正切值即可.
的平面角的余弦值,再转化为正切值即可.
证明:(1)∵在四棱锥![]() 中,
中,![]() 平面
平面![]() .
.![]() ,
, ![]() ,
,![]() .点
.点![]() 是
是![]() 与
与![]() 的交点,
的交点,![]() ,
,
∴在正三角形![]() 中,
中,![]() ,
,
在![]() 中,∵
中,∵![]() 是
是![]() 中点,
中点,![]() ,
,![]() ,又
,又![]() ,
,![]() ,
,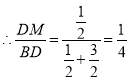 ,
,
∵点![]() 在线段
在线段![]() 上且
上且![]() ,
,
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)![]() ,
,
分别以![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图的空间直角坐标系,
轴建立如图的空间直角坐标系,
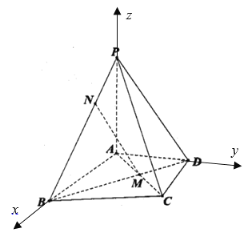
 ,
,
![]() ,
,
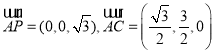 ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则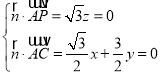 ,取
,取![]() ,得
,得![]() ,
,
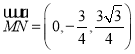 ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则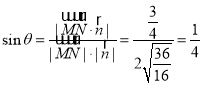 ,
,
故直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ;
;
(3)由(2)可知,![]() 为平面
为平面![]() 的法向量,
的法向量,
![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则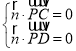 ,即
,即 ,
,
令![]() ,解得
,解得![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,则
,则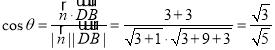 ,
,
![]()
故二面角![]() 的正切值为
的正切值为![]() .
.

练习册系列答案
相关题目
【题目】某企业生产甲、乙两种产品均需要![]() ,
,![]() 两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获得利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获得利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
甲 | 乙 | 原料限额 | |
| 3 | 2 | 10 |
| 1 | 2 | 6 |
A. 10万元B. 12万元C. 13万元D. 14万元