题目内容
.已知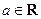 ,函数
,函数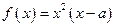 .
.
(1)若函数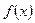 在区间
在区间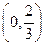 内是减函数,求实数
内是减函数,求实数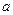 的取值范围;
的取值范围;
(2)求函数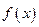 在区间
在区间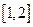 上的最小值
上的最小值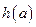 ;
;
(3)对(2)中的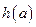 ,若关于
,若关于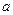 的方程
的方程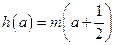 有两个不相等的实数解,
有两个不相等的实数解,
求实数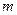 的取值范围.
的取值范围.
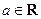 ,函数
,函数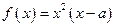 .
.(1)若函数
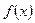 在区间
在区间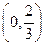 内是减函数,求实数
内是减函数,求实数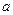 的取值范围;
的取值范围;(2)求函数
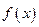 在区间
在区间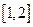 上的最小值
上的最小值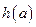 ;
;(3)对(2)中的
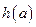 ,若关于
,若关于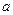 的方程
的方程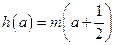 有两个不相等的实数解,
有两个不相等的实数解,求实数
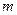 的取值范围.
的取值范围.解:∵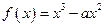 ,∴
,∴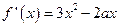 .………………………1分
.………………………1分
∵函数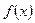 在区间
在区间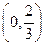 内是减函数,∴
内是减函数,∴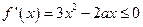 在
在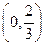 上恒成立.…………2分
上恒成立.…………2分
即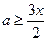 在
在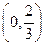 上恒成立,……………………………………………………3分
上恒成立,……………………………………………………3分
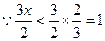 ,∴
,∴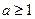 .
.
故实数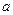 的取值范围为
的取值范围为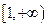 .………………………………………………4分
.………………………………………………4分
(2)解:∵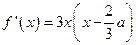 ,令
,令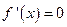 得
得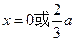 .………………5分
.………………5分
①若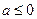 ,则当
,则当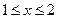 时,
时,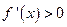 ,所以
,所以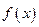 在区间
在区间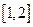 上是增函数,
上是增函数,
所以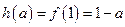 .………………………………………………6分
.………………………………………………6分
②若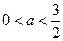 ,即
,即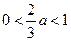 ,则当
,则当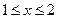 时,
时,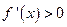 ,所以
,所以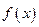 在区间
在区间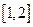 上是增函数,
上是增函数,
所以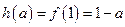 .……………………………………………7分
.……………………………………………7分
③若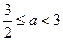 ,即
,即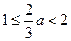 ,则当
,则当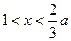 时,
时,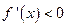 ;当
;当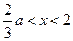 时,
时,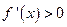 .
.
所以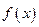 在区间
在区间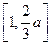 上是减函数,在区间
上是减函数,在区间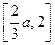 上是增函数.
上是增函数.
所以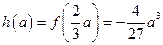 .………………………………………8分
.………………………………………8分
④若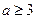 ,即
,即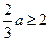 ,则当
,则当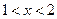 时,
时,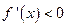 ,所以
,所以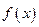 在区间
在区间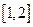 上是减函数.
上是减函数.
所以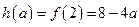 .……………………………………………9分
.……………………………………………9分
综上所述,函数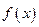 在区间
在区间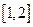 的最小值
的最小值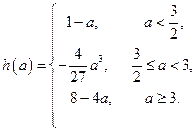 ……………10分
……………10分
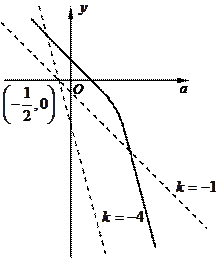 (3)解:由题意
(3)解:由题意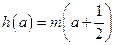 有两个不相等的实数解,
有两个不相等的实数解,
即(2)中函数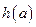 的图像与直线
的图像与直线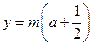 有两个
有两个
不同的交点.…………………………………………………………11分
而直线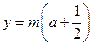 恒过定点
恒过定点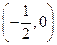 ,
,
由右图知实数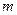 的取值范围是
的取值范围是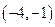 .…………………………14分
.…………………………14分
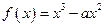 ,∴
,∴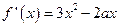 .………………………1分
.………………………1分∵函数
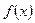 在区间
在区间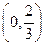 内是减函数,∴
内是减函数,∴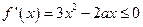 在
在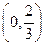 上恒成立.…………2分
上恒成立.…………2分即
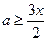 在
在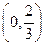 上恒成立,……………………………………………………3分
上恒成立,……………………………………………………3分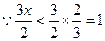 ,∴
,∴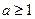 .
.故实数
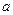 的取值范围为
的取值范围为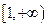 .………………………………………………4分
.………………………………………………4分(2)解:∵
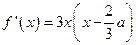 ,令
,令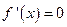 得
得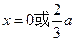 .………………5分
.………………5分①若
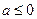 ,则当
,则当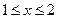 时,
时,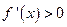 ,所以
,所以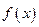 在区间
在区间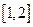 上是增函数,
上是增函数,所以
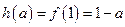 .………………………………………………6分
.………………………………………………6分②若
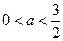 ,即
,即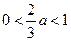 ,则当
,则当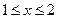 时,
时,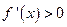 ,所以
,所以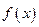 在区间
在区间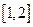 上是增函数,
上是增函数,所以
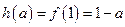 .……………………………………………7分
.……………………………………………7分③若
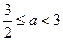 ,即
,即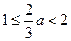 ,则当
,则当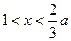 时,
时,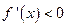 ;当
;当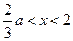 时,
时,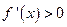 .
.所以
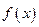 在区间
在区间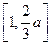 上是减函数,在区间
上是减函数,在区间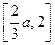 上是增函数.
上是增函数.所以
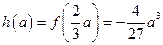 .………………………………………8分
.………………………………………8分④若
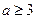 ,即
,即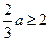 ,则当
,则当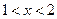 时,
时,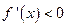 ,所以
,所以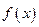 在区间
在区间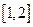 上是减函数.
上是减函数.所以
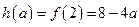 .……………………………………………9分
.……………………………………………9分综上所述,函数
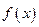 在区间
在区间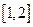 的最小值
的最小值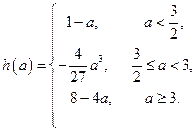 ……………10分
……………10分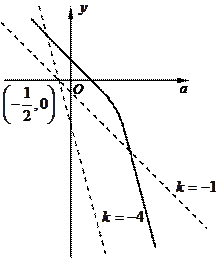 (3)解:由题意
(3)解:由题意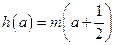 有两个不相等的实数解,
有两个不相等的实数解,即(2)中函数
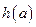 的图像与直线
的图像与直线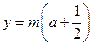 有两个
有两个不同的交点.…………………………………………………………11分
而直线
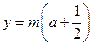 恒过定点
恒过定点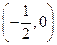 ,
,由右图知实数
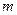 的取值范围是
的取值范围是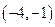 .…………………………14分
.…………………………14分略

练习册系列答案
相关题目
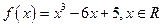
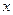 的方程
的方程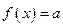 有三个不同的实根,求实数
有三个不同的实根,求实数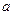 的取值范围。
的取值范围。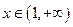 时,
时,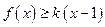 恒成立。求实数
恒成立。求实数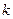 的取值范围。
的取值范围。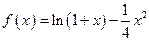 ;
;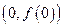 处的切线方程;
处的切线方程;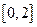 上的最大值和最小值.
上的最大值和最小值.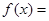
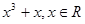 ,当0
,当0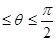 时,
时,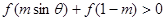 恒成立,则实数
恒成立,则实数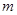 的取值范围是 ( )
的取值范围是 ( )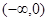
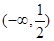
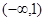
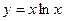 的单调递减区间是(
的单调递减区间是( )
)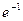 ,+∞)
,+∞)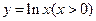 的图象与直线
的图象与直线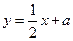 相切,则
相切,则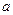 等于( )
等于( )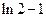
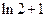

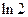
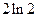
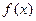 =
=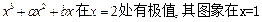 处的
处的 切线平行于直线
切线平行于直线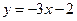 ,试求函数
,试求函数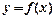 的图象在点P处的切线方程是
的图象在点P处的切线方程是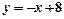 ,则
,则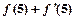 =
=  .
.