题目内容
15.设n∈N,且n>0,试用数学归纳法证明1+21+22+23+…+23n-1 能被31整除.分析 当n=1时,1+21+22+23+…+25n-1=31能被31整除,假设n=k时,1+21+22+23+…+25n-1 能被31整除,则则n=k+1时,1+21+22+23+…+23(k+1)-1也能被31整除,综合可得结论.
解答 证明:当n=1时,1+21+22+23+…+25n-1=1+21+22+23+24=25-1=31能被31整除,
假设n=k时,1+21+22+23+…+25n-1 能被31整除,
不妨令1+21+22+23+…+25k-1=31a,a∈Z,
则n=k+1时,
1+21+22+23+…+23(k+1)-1
=1+21+22+23+…+25k-1+25k+25k+1+25k+2+25k+3+25k+4
=31a+25k+25k+1+25k+2+25k+3+25k+4
=31a+25k(1+21+22+23+24)
=31a+31•25k也能被31整除,
综上所述n∈N,且n>0时,1+21+22+23+…+23n-1 能被31整除.
点评 本题考查的知识点是数学归纳法,熟练掌握数学归纳的证明步骤是解答的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
5.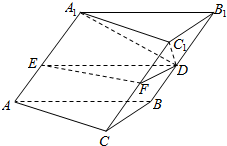 已知斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱长为5,点D,E,F分别是BB1,AA1,CC1,的中点,若侧棱AA1与底面三角形的相邻两边都成60°角,则四棱锥D-A1C1EF的体积是( )
已知斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱长为5,点D,E,F分别是BB1,AA1,CC1,的中点,若侧棱AA1与底面三角形的相邻两边都成60°角,则四棱锥D-A1C1EF的体积是( )
 已知斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱长为5,点D,E,F分别是BB1,AA1,CC1,的中点,若侧棱AA1与底面三角形的相邻两边都成60°角,则四棱锥D-A1C1EF的体积是( )
已知斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱长为5,点D,E,F分别是BB1,AA1,CC1,的中点,若侧棱AA1与底面三角形的相邻两边都成60°角,则四棱锥D-A1C1EF的体积是( )| A. | $\frac{{20\sqrt{2}}}{3}$ | B. | $\frac{{20\sqrt{3}}}{3}$ | C. | $\frac{{50\sqrt{2}}}{9}$ | D. | $\frac{{50\sqrt{3}}}{9}$ |