题目内容
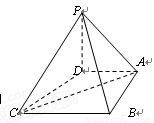
在四棱锥![]() 中,底面
中,底面![]() 是一直角梯形,
是一直角梯形,![]() ,
,![]() 与底面成
与底面成![]() 角. (1)若
角. (1)若![]() 为垂足,求证:
为垂足,求证:![]() ; (2)在(1)的条件下,求异面直线
; (2)在(1)的条件下,求异面直线![]() 与
与![]() 所成角的余弦值; (3)求平面
所成角的余弦值; (3)求平面![]() 与平面
与平面![]() 所成的锐二面角的正切值.
所成的锐二面角的正切值.
(本小题主要考查空间线线关系、面面关系、空间向量及坐标运算等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力)
解法一:(1)![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() …………4分
…………4分
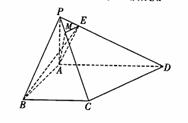
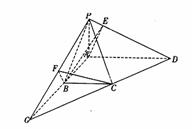
(2)过点![]() 作
作![]() 交
交![]() 于
于![]() ,连结
,连结![]() ,
,
则![]() 与
与![]() 所成角即为
所成角即为![]() 与
与![]() 所成角.
所成角.
![]()
![]()
![]()
![]()
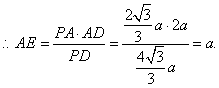
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
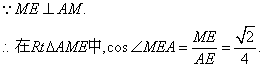
∴异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() . …………9分
. …………9分
(3)延长![]() 与
与![]() 相交于
相交于![]() 点,连
点,连![]() ,
,
则面![]() 与面
与面![]() 的交线为
的交线为![]() ,易知
,易知![]() ⊥平面
⊥平面![]() ,
,
过![]() 作
作![]() ,
,
![]() ,
,
![]() ,
,
![]()

∴平面![]() 与平面
与平面![]() 所成的二面角的正切值为2. ……14分
所成的二面角的正切值为2. ……14分
解法二:(1)如图建立空间直角坐标系,
![]()
![]()
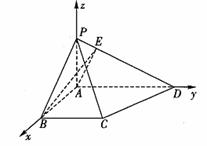
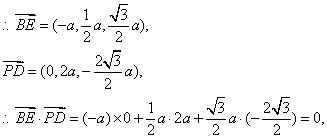
![]() …………4分
…………4分
(2)由(1)知,![]()
![]()
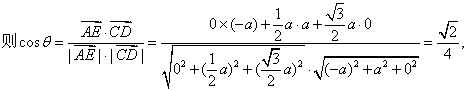
∴异面直线![]() 与
与![]() 所成角的余统值为
所成角的余统值为![]() . …………9分
. …………9分
(3)易知,![]()
则![]()
![]() 的法向量.
的法向量.
![]()

∴平面PAB与平面PCD所成锐二面角的正切值为2. …………14分

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目


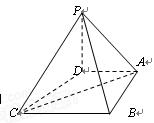
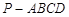 中,底面
中,底面 是一直角梯形,
是一直角梯形,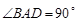 ,
,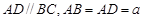 ,
,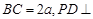 底面
底面 的体积;
的体积;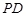 上是否存在一点
上是否存在一点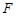 ,使得
,使得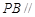 平面
平面 ,若存在,求出
,若存在,求出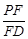 的值;若不存在,试说明理由.
的值;若不存在,试说明理由.