题目内容
（本小题满分12分）
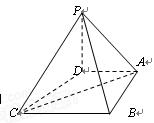
在四棱锥
中，底面
是一直角梯形，
，
，
底面．
（1）在
上是否存在一点
，使得
平面
，若存在，求出
的值；
若不存在，试说明理由；
（2）在（1）的条件下，若
与
所成的角为
，求二面角
的余弦值．
（1）
，理由见解析。
（2）
解析:
（1）方法一：存在点
使
平面
，
…………………………1分
连接
交
于
，连接
，
，所以
，所以
…4分
又
平面，
不在平面内，所以平面…………………………5分
方法二：建立如图所示的空间直角坐标系，
，
，
，
，…1分
设
，则
，假设存在点使平面，
………2分
设平面的一个法向量为
，
，
，
，所以
，
……4分 所以……5分
（2）
，
，因为
与
所成的角为
所以
，则
……………7分
由（1）知平面的一个法向量为
…………………………8分[来源:学科网ZXXK]
因为
，
，所以
所以
，所以
，又
底面
，则
平面
，
所以
是平面的一个法向量…………………………10分
所以
，所以二面角的余弦值为…………12分
练习册系列答案
全能测控期末小状元系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
