题目内容
4.在下列函数中,图象关于原点对称的是( )| A. | y=xsinx | B. | y=$\frac{{e}^{x}+{e}^{-x}}{2}$ | C. | y=xlnx | D. | y=x3-2sinx+tanx |
分析 由条件判断各个选项中函数的奇偶性,再根据奇函数的图象特征,得出结论.
解答 解:由于y=xsinx、y=$\frac{{e}^{x}+{e}^{-x}}{2}$ 都是偶函数,它们的图象关于y轴对称,故排除A、B;
由于y=xlnx的定义域为(0,+∞),不关于原点对称,故此函数为非奇非偶函数,它的图象不关于原点对称,故排除C.
由于y=x3-2sinx+tanx为奇函数,它的图象关于原点对称,
故选:D.
点评 本题主要考查函数的奇偶性的判断,奇、偶函数的性质,属于中档题.

练习册系列答案
相关题目
19.在平行四边形ABCD中,$\overrightarrow{AC}$=(-3,4),$\overrightarrow{BD}$=(3,2),则四边形ABCD的面积为( )
| A. | 8 | B. | 18 | C. | $\sqrt{13}$ | D. | 2$\sqrt{13}$ |
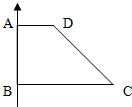 如图1,直角梯形ABCD中,∠A=∠B=90°,AD∥BC,AD=2,AB=3,BC=6,把直角梯形ABCD绕边AB旋转一周得到一个旋转体,求:
如图1,直角梯形ABCD中,∠A=∠B=90°,AD∥BC,AD=2,AB=3,BC=6,把直角梯形ABCD绕边AB旋转一周得到一个旋转体,求: