题目内容
已知在数列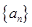 和
和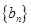 中,
中,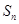 为数列
为数列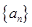 的前
的前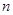 项和,
项和,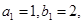 且
且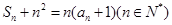 ,
,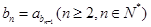 .
.
(Ⅰ)求数列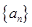 和
和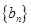 的通项公式;
的通项公式;
(Ⅱ)设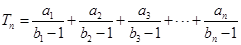 ,求
,求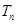 .
.
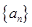 和
和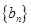 中,
中,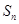 为数列
为数列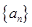 的前
的前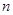 项和,
项和,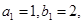 且
且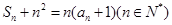 ,
,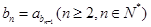 .
.(Ⅰ)求数列
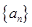 和
和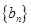 的通项公式;
的通项公式;(Ⅱ)设
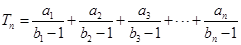 ,求
,求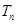 .
.(Ⅰ)故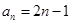 (
( ),
),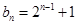
 ;(Ⅱ)
;(Ⅱ) .
.
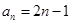 (
( ),
),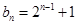
 ;(Ⅱ)
;(Ⅱ) .
.本试题主要是考查了通项公式与前n项和之间的关系式,以及运用递推关系求解数列的通项公式的运用和求和的运用。
(1) 时,
时,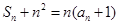 ,
,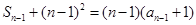
两式相减得: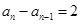 (
( ),
),
故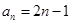 (
( )
)
(2)
则利用错位相减法得到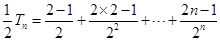 ,从而得到
,从而得到

解:(Ⅰ) 时,
时,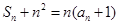 ,
,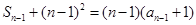
两式相减得: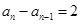 (
( ),
),
故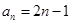 (
( )
)
经检验, 时上式成立,所以
时上式成立,所以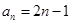

由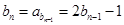 ,得:
,得: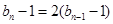 (
( )
)
故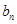 =
=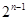 +1(
+1( )
)
经检验, 时上式成立,所以
时上式成立,所以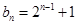

(Ⅱ)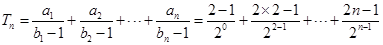
则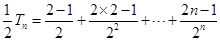
两式相减得:
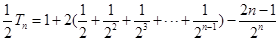

故 .
.
(1)
 时,
时,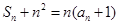 ,
,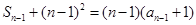
两式相减得:
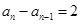 (
( ),
),故
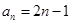 (
( )
)(2)

则利用错位相减法得到
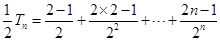 ,从而得到
,从而得到
解:(Ⅰ)
 时,
时,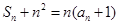 ,
,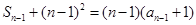
两式相减得:
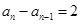 (
( ),
),故
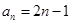 (
( )
)经检验,
 时上式成立,所以
时上式成立,所以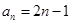

由
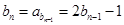 ,得:
,得: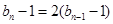 (
( )
)故
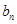 =
=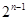 +1(
+1( )
)经检验,
 时上式成立,所以
时上式成立,所以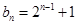

(Ⅱ)
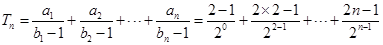
则
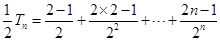
两式相减得:
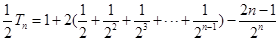

故
 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
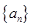 和
和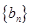 的前n项和分别为
的前n项和分别为 ,且
,且 ,则使得
,则使得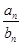 为整数的正整数n的个数是___
为整数的正整数n的个数是___ 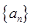 的首项为
的首项为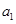 ,公差为
,公差为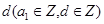 ,前
,前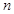 项的和为
项的和为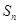 ,
,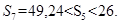
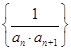 的前
的前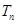 ,求
,求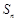 是等差数列{
是等差数列{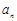 }的前n项和,且
}的前n项和,且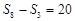 ,则
,则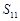 的值为
的值为 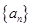 的前
的前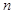 项和为
项和为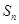 ,则下列说法错误的是 .
,则下列说法错误的是 .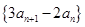 是等差数列;
是等差数列;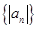 是等差数列;
是等差数列;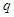 的等比数列,则
的等比数列,则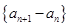 也是等比数列且公比为
也是等比数列且公比为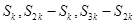
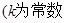
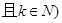 也是等比数列且公比为
也是等比数列且公比为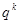 .
.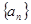 是等差数列,
是等差数列,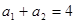 ,
,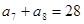 ,则该数列的前10项和
,则该数列的前10项和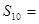
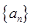 为等差数列,且
为等差数列,且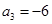 ,
,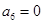 。
。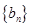 满足
满足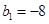 ,
,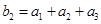 ,求数列
,求数列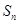 。
。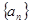 中,
中,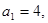
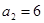 ,且
,且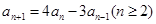
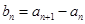 ,求数列
,求数列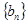 的通项公式;
的通项公式;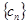 中,
中,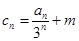 ,且
,且 的值及
的值及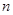 项和.
项和.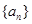 的前n项和为
的前n项和为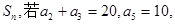 则S5等于
则S5等于