题目内容
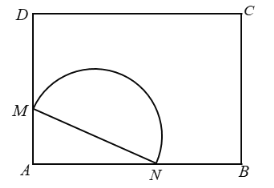
【题目】如图,在市中心有一矩形空地![]() .市政府欲将它改造成绿化景观带,具体方案如下:在边
.市政府欲将它改造成绿化景观带,具体方案如下:在边![]() 上分别取点M,N,在三角形
上分别取点M,N,在三角形![]() 内建造假山,在以
内建造假山,在以![]() 为直径的半圆内建造喷泉,其余区域栽种各种观赏类植物.
为直径的半圆内建造喷泉,其余区域栽种各种观赏类植物.
(1)若假山区域面积为![]() ,求喷泉区域面积的最小值;
,求喷泉区域面积的最小值;
(2)若![]() ,求假山区域面积的最大值.
,求假山区域面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)设![]() ,半圆的直径
,半圆的直径![]() ,根据假山区域面积为
,根据假山区域面积为![]() ,找到
,找到![]() 与
与![]() 的关系,再表示出喷泉区域面积,求最值,注意验证半圆是否在矩形空地
的关系,再表示出喷泉区域面积,求最值,注意验证半圆是否在矩形空地![]() 内,即验证是否能取到最小值;
内,即验证是否能取到最小值;
(2)由(1)根据以![]() 为直径的半圆区域在矩形广场内,求得
为直径的半圆区域在矩形广场内,求得![]() 的范围,再将假山区域面积用
的范围,再将假山区域面积用![]() 表示出来,再求最值.
表示出来,再求最值.
解:(1)设![]() ,半圆的直径
,半圆的直径![]() ,半圆的圆心为O.
,半圆的圆心为O.
在直角三角形![]() 中,
中,![]() ,所以
,所以![]() .
.
因为假山区域面积为![]() ,
,
所以![]()
所以![]() ,所以喷泉区域面积
,所以喷泉区域面积![]() ,
,
当且仅当![]() ,即
,即![]() 时取等号.此时
时取等号.此时![]() .
.
因为点O到![]() 的距离
的距离![]() ,点O到
,点O到![]() 的距离
的距离![]() ,
,
所以![]() ,即
,即![]() ,
,
![]() ,即
,即![]() .
.
所以以![]() 为直径的半圆区域一定在矩形广场内.
为直径的半圆区域一定在矩形广场内.
所以当![]() 时,
时,![]() 取得最小值
取得最小值![]() .
.
喷泉区域面积的最小值为![]() .
.
(2)由(1)知,若![]() ,则
,则![]() .
.
所以点O到![]() 的距离
的距离![]() ,
,
点O到![]() 的距离
的距离![]() ,
,
因为以![]() 为直径的半圆区域在矩形广场内,
为直径的半圆区域在矩形广场内,
所以![]() 即
即![]() 所以
所以![]() .
.
又因为![]() ,所以
,所以![]() .
.
所以假山区域面积![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以当![]() 时,假山区域面积的最大值为
时,假山区域面积的最大值为![]() .
.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案
相关题目