题目内容
已知函数f(x)=sin x+tan x,项数为27的等差数列{an}满足an∈(-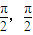 ),且公差d≠0,若f(a1)+f(a2)+…f(a27)=0,则当k= 时,f(ak)=0.
),且公差d≠0,若f(a1)+f(a2)+…f(a27)=0,则当k= 时,f(ak)=0.
【答案】分析:本题考查的知识点是函数的奇偶性及对称性,由函数f(x)=sin x+tan x,项数为27的等差数列{an}满足an∈(-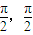 ),且公差d≠0,若f(a1)+f(a2)+…f(a27)=0,我们易得a1,a2,…,a27前后相应项关于原点对称,则f(a14)=0,易得k值.
),且公差d≠0,若f(a1)+f(a2)+…f(a27)=0,我们易得a1,a2,…,a27前后相应项关于原点对称,则f(a14)=0,易得k值.
解答:解:因为函数f(x)=sinx+tanx是奇函数,
所以图象关于原点对称,图象过原点.
而等差数列{an}有27项,an∈(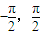 ).
).
若f(a1)+f(a2)+f(a3)+…+f(a27)=0,
则必有f(a14)=0,
所以k=14.
故答案为:14
点评:代数的核心内容是函数,函数的定义域、值域、性质均为高考热点,所有要求同学们熟练掌握函数特别是基本函数的图象和性质,并能结合平移、对称、伸缩、对折变换的性质,推出基本函数变换得到的函数的性质.
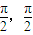 ),且公差d≠0,若f(a1)+f(a2)+…f(a27)=0,我们易得a1,a2,…,a27前后相应项关于原点对称,则f(a14)=0,易得k值.
),且公差d≠0,若f(a1)+f(a2)+…f(a27)=0,我们易得a1,a2,…,a27前后相应项关于原点对称,则f(a14)=0,易得k值.解答:解:因为函数f(x)=sinx+tanx是奇函数,
所以图象关于原点对称,图象过原点.
而等差数列{an}有27项,an∈(
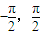 ).
).若f(a1)+f(a2)+f(a3)+…+f(a27)=0,
则必有f(a14)=0,
所以k=14.
故答案为:14
点评:代数的核心内容是函数,函数的定义域、值域、性质均为高考热点,所有要求同学们熟练掌握函数特别是基本函数的图象和性质,并能结合平移、对称、伸缩、对折变换的性质,推出基本函数变换得到的函数的性质.

练习册系列答案
相关题目
