题目内容
12.设a,b为两条不同的直线,α,β为两个不重合的平面.下列命题中正确的是( )| A. | 若α⊥β,a⊥α,则a∥β | |
| B. | 若a,b与α所成的角相等,则a与b平行或相交 | |
| C. | 若α内有三个不共线的点到β的距离相等,则α∥β | |
| D. | 若α∩β=b,a?α且a∥β,则a∥b |
分析 A.由已知可得a∥β或a?β,即可判断出正误;
B.由已知可得a与b平行或相交或为异面直线,即可判断出正误;
C.由已知可得α∥β或相交,即可判断出正误;
D.利用线面平行、线线平行的判定与性质定理即可得出.
解答 解:A.若α⊥β,a⊥α,则a∥β或a?β,因此不正确;
B.a,b与α所成的角相等,则a与b平行或相交或为异面直线,因此不正确;
C.若α内有三个不共线的点到β的距离相等,则α∥β或相交,因此不正确;
D.若α∩β=b,a?α且a∥β,则a∥b,正确.
故选:D.
点评 本题考查了空间中线面位置关系,考查了空间想象能力与推理能力,属于中档题.

练习册系列答案
相关题目
3.经统计,在银行一个营业窗口每天上午9点钟排队等候的人数及相应概率如下:
则该营业窗口上午9点钟时,至少有2人排队的概率是0.74.
| 排队人数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
| 概率 | 0.1 | 0.16 | 0.3 | 0.3 | 0.1 | 0.04 |
20.某女士为将体重维持在正常水平,每天坚持体育锻炼.已知该女士某星期一测得其体重是50kg,而后每天测得的体重与前一天相比,或减少0.5kg或维持不变或增加0.5kg,若该星期天该女士测得其体重仍然是50kg,则该女士在这个星期内每天测得的体重的所有可能结果有( )
| A. | 121种 | B. | 141种 | C. | 231种 | D. | 282种 |
17.已知$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个顶点和一个焦点在圆x2+y2-x-y-6=0上,则双曲线的虚轴长为( )
| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | 4$\sqrt{3}$ | D. | 4$\sqrt{5}$ |
1.执行如图所示的程序框图,若输入的n∈{1,2,3},则输出的s属于( )


| A. | {1,2} | B. | {1,3} | C. | {2,3} | D. | {1,3,9} |
2.设集合M={x||x+1|<3,x∈R},N={0,1,2},则M∩N=( )
| A. | {0,1} | B. | {0,1,2} | C. | {x|0<x<2} | D. | {x|-4<x<2} |
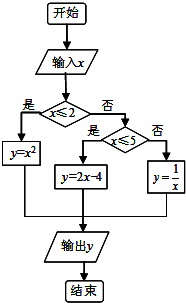 如图给出了一个程序框图,其作用是输入x的值输出相应的y值,若要使输入的x值与输出的y值相等,则这样的x值的个数是3.
如图给出了一个程序框图,其作用是输入x的值输出相应的y值,若要使输入的x值与输出的y值相等,则这样的x值的个数是3. 在三棱锥C-ABD中(如图),△ABD与△CBD是全等的等腰直角三角形,O为斜边BD的中点,AB=4,二面角A-BD-C的大小为60°,并给出下面结论:
在三棱锥C-ABD中(如图),△ABD与△CBD是全等的等腰直角三角形,O为斜边BD的中点,AB=4,二面角A-BD-C的大小为60°,并给出下面结论: